Logaritmos

por Huan_ Sex 13 Jul 2012, 01:59

Certa população de bactérias tem seu crescimento populacional representado pela função 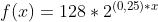$Logaritmos Gif$
em que x é o tempo em dias a partir do início da observação. Para
encontrar o número de dias de observação a partir da população de
bactérias, pode-se usar a relação g(x) representada por

Spoiler:

por **Al.Henrique** Sex 13 Jul 2012, 04:05

Faltou definir quem é g(x)..

por Huan_ Sex 13 Jul 2012, 12:33

Al.Henrique escreveu:Faltou definir quem é g(x)..

f(x) é em relção ao tempo, tem que relacionar f(x) com g(x) e econtrar g(x) que represente uma quantidade.

por **Elcioschin** Sex 13 Jul 2012, 13:12

Huan

Não deu para entender.
Por favor, coloque o enunciado COMPLETO

por Huan_ Sex 13 Jul 2012, 13:36

Elcioschin escreveu:Huan

Não deu para entender.
Por favor, coloque o enunciado COMPLETO

Elcioschin, olhe ai o enunciado completo pra vê se mudou alguma coisa.

Desculpa não ter colocado antes é que achei que ficaria mais claro dá forma que eu coloquei

por **Elcioschin** Sex 13 Jul 2012, 16:43

Huan

Por favor, nunca faça isto novamente.

Um enunciado deve sempre ser colocado literalmente, sem modificações.

Assim fazendo você colocou APENAS a sua interpretação, e, convenhamos, confundiu tudo e todos

f(x) = 128*2^(0,25*x) ----> Aplicando logaritmo na base 2:

log2[(f)x)] = log2[128*2^(0,25)*x]

log2[(f)x)] = log2[128] + log2[2^(0,25)*x]

log2[(f)x)] = log2[2^7] + log2[2^(0,25)*x]

log2[(f)x)] = 7*log2[2] + 0,25*x*log2[2] ----> log2[2] = 1

log2[f(x)] = 7 + x/4 ---> 4*log2[f(x)] + 28 + x ---> x = 4*log2[f(x)] - 28

por Huan_ Qui 02 Ago 2012, 01:04

Desculpa, mestre Elcioschin, por ta revivendo o tópico depois de tanto tempo, mas ainda tenho dúvidas...

Você terminou aqui,

x = 4*log2[f(x)] - 28

Eu substitui f(x) de acordo, mas eu não consegui chegar no gabarito:

$g(x)= 4 \; log_2 \; \left (\frac{x}{128 \right )}$

por **Elcioschin** Qui 02 Ago 2012, 09:34

Huan

É praticamente a mesma coisa:

x = 4*log2f(x) - 28 ---> x = 4*log2f(x) - 4*7 ---> x = 4*log2f(x) - 4*log2(2^7) --->

x = 4*log2f(x) - 4*log2128 ---> x = 4*[log2f(x) - log2(128)] ---> x = 4*log2[f(x)/128] ---->

Calculando a inversa, substitui-se x por g(x) e f(x) por x: g(x) = 4*log2(x/128)

Agora veja: se você tivesse colocado o gabarito JUNTO com o enunciado, eu teria chegado nele.

Por favor, coloque SEMPRE o gabarito: isto ajuda a quem pretende ajudá-lo.