Geometria - Área de um triângulo

por **raimundo pereira** Qui 21 Jun 2012, 20:34

Calcular a área do triângulo isósceles ABC, sabendo que o raio do círculo O' é 13m e que a distância dos centros OO' = 19m.
R: 924 m²

Fonte: Exercícios Geometria - Edgar Filho

Geometria - Área de um triângulo 33ys7bn

Geometria - Área de um triângulo 33ys7bn

obs: os lados do triângulo são tangentes aos círculos.

por **Medeiros** Dom 01 Jul 2012, 21:58

Qual o comprimento do segmento tangente?

Geometria - Área de um triângulo Areadotriangulo1

OD⊥DE e O'E⊥DE -----> OD║O'E
DF║O'O
Pitágoras no ∆DEF, retângulo em E, vem:
x² = (R+r)² - (R-r)² -----> x² = 2R.2r -----> x² = 4Rr -----> ${\color{Red} x=2\sqrt{Rr}}$

Geometria - Área de um triângulo Areadotriangulo2

traçamos JK║GH║BC, com JK e GH tangentes às circunferências.

Considerando o ponto H em relação a:
-- a circunferência O' -----> HD = HI
-- a circunferência O -----> HE = HI
⇒ HD = HE = x/2
Por simetria, GI=HI ⇒ GH=DE=x

os trapézios isósceles BCHG~GHKJ -----> 12/26 = x/BC -----> BC = 13x/6

∆AGH ~ ∆ABC
GH/BC = (H-26)/H -----> x/(13x/6) = (H-26)/H -----> 6/13 = (H-26)/H
6H = 13H - 2*13² -----> H = 2*13²/7

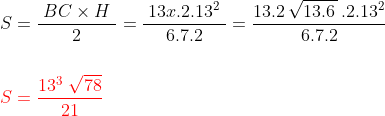
$\\S=\frac{\;BC\times H\;}{2} = \frac{\;13x.2.13^2\;}{6.7.2} = \frac{13.2\,\sqrt{13.6\,}\,.2.13^2}{6.7.2} \\\\\\ {\color{Red} S = \frac{13^3\;\sqrt{78}}{21}}$

realizando a conta ......... S = 923,970... ≈ 924 m²