Área hachurada

por theblackmamba Sex 20 Jan 2012, 00:22

Na figura, AM = MB, CN = CA/3 e BP = BC/4. Se o triângulo ABC tem área S, ache a área hachurada.

por **adriano tavares** Qua 25 Jan 2012, 15:57

Olá,theblackmamba.

[img]

[/img]

Os triângulos ABP e APC têm mesma altura,sendo PC o quádruplo de PB tem-se que:

$A_{APC}=\frac{4}{5}S$

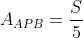
$A_{APB}=\frac{S}{5}$

Vamos calcular a razão entre os segmentos TA e TP aplicando o teorema de Menelaus no triângulo APB considerando a transversal MC.

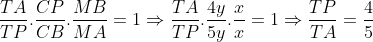
$\frac{TA}{TP}.\frac{CP}{CB}.\frac{MB}{MA}=1 \Rightarrow \frac{TA}{TP}.\frac{4y}{5y}.\frac{x}{x}=1 \Rightarrow \frac{TP}{TA}=\frac{4}{5}$

Vamos calcular a razão entre os segmentos KC e KM aplicando o teorema de Menelaus no triângulo CMA considerando a transversal NB.

$A_{CTP}=\frac{4}{9}.\frac{4}{5}S \Rightarrow A_{CTP}=\frac{16}{45}S$

$A_{CTA}=\frac{5}{9}.\frac{4}{5}S \Rightarrow A_{CTA}=\frac{4}{9}S$

$\frac{KC}{KM}.\frac{BM}{BA}.\frac{AN}{NC}=1 \Rightarrow \frac{KC}{KM}.\frac{x}{2x}.\frac{3a}{a}=1 \Rightarrow \frac{KC}{KM}=\frac{2}{3}$

Note que os triângulos CMB e CMA têm mesma área, pois ambos têm mesma base e mesma altura.

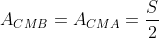
$A_{CMB}=A_{CMA}=\frac{S}{2}$

Considerando a base MC do triângulo CMB vamos calcular a área do triângulo KBC.

$A_{KBC}=\frac{2}{5}.\frac{S}{2} \Rightarrow A_{KBC}=\frac{S}{5}$

Cálculo da área do triângulo ATM:

$A_{ATM}=A_{CMA}-A_{CTA}\Rightarrow A_{ATM}=\frac{S}{2}-\frac{4}{9}S \Rightarrow A_{ATM}=\frac{S}{18}$

Vamos calcular a razão entre os segmentos AZ e ZP aplicando o teorema de Menelaus no triângulo APC considerando a transversal NB.

$\frac{AZ}{ZP}.\frac{BP}{BC}.\frac{CN}{NA}=1\Rightarrow \frac{AZ}{ZP}.\frac{y}{5y}.\frac{a}{3a}=1\Rightarrow \frac{ZP}{AZ}=\frac{1}{15}$

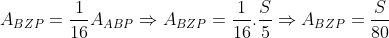
$A_{BZP}=\frac{1}{16}A_{ABP}\Rightarrow A_{BZP}=\frac{1}{16}.\frac{S}{5}\Rightarrow A_{BZP}=\frac{S}{80}$

$A_{ZKCP}=A_{KBC}-A_{BZP}\Rightarrow A_{ZKCP}=\frac{S}{5}-\frac{S}{80} \Rightarrow A_{ZKCP}=\frac{3}{16}S$

$A_{ZTK}=A_{CTP}-A_{ZKCP}\Rightarrow A_{ZTK}=\frac{16}{45}S-\frac{3}{16}S \Rightarrow A_{ZTK}=\frac{121}{720}S$

por theblackmamba Qui 26 Jan 2012, 11:18

Adriano muito obrigado mesmo...Abraço

por bianca10lima Qui 26 Jan 2012, 14:46

Olá, Adriano!
Gostaria de te perguntar umas coisinhas...( sou bem lerda, então me desculpe..)
- A primeira coisa é de como você descbobriu que a área de Aapc tem 4x a área de Aapb.
- a segunda coisa é sobre como você chegou( na primeira parte) que TA/TP * 4y/5y *x/x = 1
- A terceira é como você descobriu que Actp = 4/9*4/5*S e Acta = 5/9*4/5*S .
-A quarta dúvida (me desculpa de VERDADE a burrice!) é porque Akbc= 2/5*s/2...
A quinta dúvida é o motivo de que pra achar a área do triângulo Aatm é a diferença entre as áreas dos triãngulos Acma e Acta.
-Sexta e última dúvida: Qual é o motivo do uso do teorema de menelaus?

Sou muito lerda com geometria analítica, acho muito difícil! :/

Desculpa ter pedido pra você explicar quase a questão inteira! :O

Obrigada, viu? hee por aturar todas essas minhas perguntas! =D

por **Elcioschin** Qui 26 Jan 2012, 15:25

bianca

Este problema não tem nada a ver com Geometria Analítica. è um problema de Geometria Plana.

1) Enunciado: BP = BC/4 ----> BP = y ----> BC = 4y

Veja agora os triângulos ABP e ACP: eles tem a mesma altura e base BP e BC

S = b*h/2 -----> SABP = y*h/2 ----> SACP = 4(y*h/2) ----> SACP = 4*SABP

2) É o teorema de Menelaus (parece que vc não conhece, então sugiro estudá-lo)

O resto é pura Álgebra

por bianca10lima Qui 26 Jan 2012, 16:33

aaaah! Agora fez sentido!
Ahaushaush verdade! É plana... mas tanto faz, sou ruim nas duas! =O
Aaah, agora já sei do que se trata o Teorema de Menelaus, e é muito funcional, eu sequer conhecia! =O
Muito obrigada pela explicação Elcioschin! =D
Ajudou bastante! =D

por Werill Qui 26 Jan 2012, 17:33

Se BP = BC/4, então onde está y e 4y, não seria, respectivamente, y e 3y?
Assim, as áreas ficariam:

Aapc = (3/4)S
Aabp = (1/4)S

__________

Também não conhecia o teorema de Manelaus Very Happy