Geometria - Pirâmide

por **Jose Carlos** Seg 28 Set 2009, 12:52

Uma pirâmide é seccionada por dois planos paralelos à base e que dividem sua altura em três partes congruentes. Obter números proporcionais aos volumes dos três sólidos em que fica dividida a pirâmide.

R: 1, 7 e 19.

por **adriano tavares** Seg 28 Set 2009, 15:26

Olá, Jose Carlos.

Geometria - Pirâmide Pirmide

por **Jose Carlos** Seg 28 Set 2009, 15:41

Olá Adriano,

Agradeço pela ótima resolução.

Um grande abraço.

por Victória Tavares Qua 01 Jul 2020, 23:30

Olá! Tem como recuperar a imagem da resolução da questão?

por Lucius Draco Qui 02 Jul 2020, 00:11

Temos:

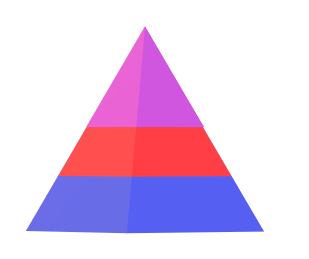
Por semelhança de pirâmides temos:

[latex]\frac{V_{1}}{V_{1}+V_{2}}=\frac{h^3}{(2h)^3}=\frac{1}{8}\Rightarrow V_{2}=7\cdot V_{1}[/latex]

e

[latex]\frac{V_{1}}{V_{1}+V_{2}+V{3}}=\frac{h^3}{(3h)^3}=\frac{1}{27}\Rightarrow \frac{V_{1}}{8\cdot V_{1}+V_{3}}=\frac{1}{27}\Rightarrow V_{3}=19\cdot V_{1}[/latex]

Portanto temos:

[latex]\left\{\begin{matrix} V_{1}=19k\\ V_{2}=7k\\ V_{3}=k \end{matrix}\right.\Rightarrow Proporcao\; 1:7:19[/latex]

por Victória Tavares Qua 08 Jul 2020, 10:40

Daria certo fazer (v1/(v1 + v2 + v3)) = k^3 ?

por **Elcioschin** Qua 08 Jul 2020, 10:55

Daria, mas o trabalho seria bem maior.

Lembre-se que a relação entre os volumes V, v de dois sólidos semelhantes, de alturas H, h é dada por:

V/v = (H/h)³

por Victória Tavares Qua 08 Jul 2020, 11:10

Aaah sim! Que legal, não sabia dessa relação.
Obrigada a todos

por **Elcioschin** Qua 08 Jul 2020, 11:15

Uma relação similar vale também para áreas de figuras semelhantes

S/s = (X/x)² ---> X e x são dimensões lineares semelhantes das figuras

Por exemplo, dois triângulos retângulos 3-4-5 (s = 6) e 6-8-10 (S = 24)

S/s = (6/3)² ---> S/s = 4 ---> S = 4.s

A estas relações dá-se o nome de homotetia ou homotesia. Pesquise!