Trigonometria - função cosseno

Bom dia! Alguém pode me ajudar a construir o gráfico da seguinte função: 
f(x) = -1 + 2.cos(x - π/2) ?

Identifiquei que o máximo, em relação à imagem, é 1 e o mínimo é -3. Quando x = 0 a função corta o eixo vertical no -1. Depois disso não consegui desenvolver e não sei muito bem o motivo, substituí π/2, π, e 3π/2 no lugar do x, mas não cheguei a lugar nenhum, estou aprendendo esse tópico ainda. Obrigado!

Tudo começa com a função f(x) = cos(x).
Você deve agora trocar o argumento por x - a. Essa operação não mexe no formato da função, somente a desloca de a para a direita. Isso porque pra alcançar, digamos cos(0), agora preciso que x = a, então cada resultado da esquerda precisa ficar mais à direita. Então, desloque cos(x) de pi/2 à direita e temos f(x) = cos(x - pi/2).



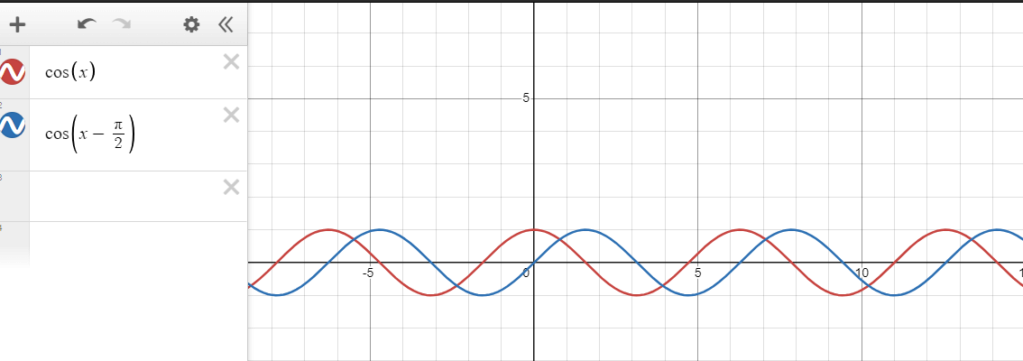
Multipliquemos por constante 2. A função 2cos(x - pi/2) é igualzinha à primeira, mas ela é mais acentuada. O período é o mesmo, mas ela vai de -2 a 2 em vez de -1 a 1 (imagine um pêndulo, é como se eu só aumentasse a amplitude, o que não muda o período). Estamos com f(x) = 2cos(x - pi/2).



Por fim, somar constante ao valor da função a desloca em y. Não é como x que é ao contrário, somar -1 é tomar a função e a jogar para baixo em 1 unidade.

Perfeito, meu amigo, obrigado!! Outra coisa, se eu multiplicasse o x da função por 2, como ficaria? Ex.: f(x) = -1 + 2.cos(2x - pi/2)

Italo01 escreveu:Perfeito, meu amigo, obrigado!! Outra coisa, se eu multiplicasse o x da função por 2, como ficaria? Ex.: f(x) = -1 + 2.cos(2x - pi/2)

Esqueci de detalhar. Vou resumir o estudo da função f(x) = k + a cos(mx + n).
k: desloca em k unidades a função na vertical
a: acentua a variação da função, aumenta a amplitude (não mexe no período)
n: desloca a função em -n unidades na horizontal (não mexe no período nem na amplitude)
m: espreme a função, diminui o período (não mexe na amplitude)
Vamos analisar o m com mais afinco. Pra que haja um período em cos(x), preciso que fique x + 2pi no argumento, daí o período é de 2pi fundamentalmente. Se eu tivesse cos(2x), bastaria x + pi -> cos(2x + 2pi), e temos um período de pi. No caso de m, façamos T o período: cos(mx + n) -> cos(m(x+T) + n) = cos(mx + mT + n). Quero que o segundo seja 2pi maior que o outro: mx + mT + n = mx + n + 2pi <=> mT = 2pi <=> T = 2pi/m. Por isso que eu digo que o m espreme a função, porque período e m são inversamente proporcionais.

Muito obrigado, cara!!

Italo01 escreveu:Muito obrigado, cara!!

Olá! Apenas para complementar o pensamento do Lipo e ajudar a agilizar a montagem da função graficamente.

f(x) = a + b.cos(cx + d)

b → Pode ser calculado pela expressão: +(P_M - P_m)/2

Onde P_M = Ponto máximo da função em y.
Onde P_m = Ponto mínimo da função em y.
O sinal positivo e negativo depende da fase da função.

c → Pode ser calculado pela expressão: T = 2∏/k

Onde T = c = Período da função.
Onde k = valor em x que completa o ciclo da função.

a e d → Representam o deslocamento vertical e horizontal do gráfico, respectivamente.

-----------------------------------------------------------------------------------------------------------

Veja um exemplo de como fica bem mais fácil assim:

No gráfico abaixo, o ponto máximo (P_M) é 4, e o ponto mínimo é 0. A função está em fase direita. Assim → + (4-0)/2 → Sua amplitude (b) é igual a 2.

O gráfico não está com valores em pi no eixo das abscissas, mas ainda dá para calcular o período (c). A função termina seu ciclo (ou seja, começa a se repetir) depois de aproximadamente 3,1415..., ou seja, pi. Assim → T = 2∏/k → T = 2∏/∏ = 2.

Por fim, a função seno, para pi = 0, tem valor 0. Como a = 2, o gráfico está 2 unidades positivas acima do eixo y. Portanto, a = 2.