Geometria Polígonos Regulares

por Lucas Lenovo Qua 24 Abr 2024, 21:38

Sobre os lados de um hexágono regular, cujo lado mede 12cm , constroem-se externamente quadrados. Unindo os vértices desses quadrados que não são do hexágono , obtém-se um dodecágono regular. Dessa forma , a medida do raio do círculo circunscrito a esse dodecágono é :
A) 6(√6 - √2)cm
B)8(√6-√2)cm
C) 6(√6+√2)cm
D)8(√6+√2)cm
E)12(√6-√2)cm

por **Medeiros** Qui 25 Abr 2024, 01:31

não desenhei os quadrados em toda a volta do hexágono, fica subentendido.

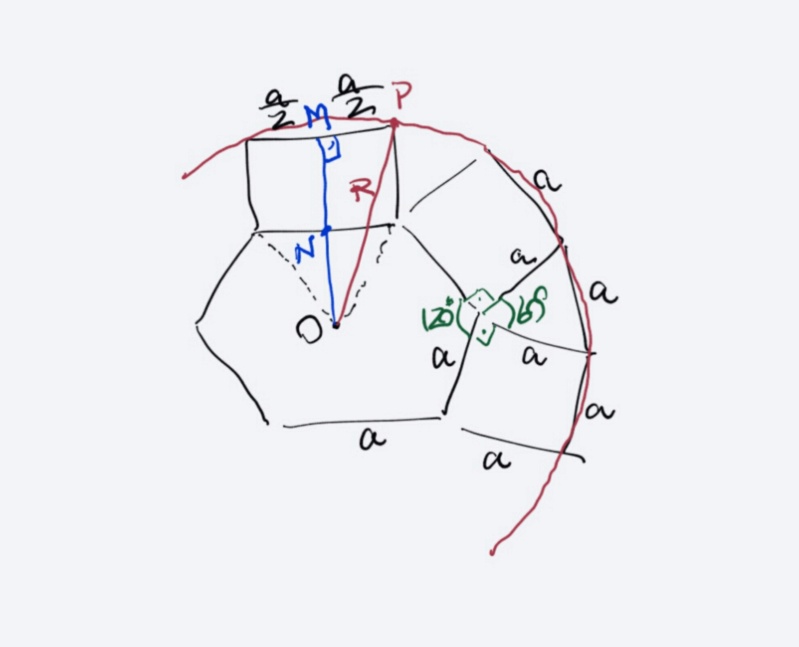
lado do hexágono = lado do quadrado = a = 12
O = baricento = circuncentro das figuras (hexágono e hexágono + adereços)
R = OP
ON = altura de triângulo equilátero de lado a -----> ON = 6√3
MN = a = 12
OM = ON + MN = 12 + 6√3 -----> OM = 6.(2 + √3)

Pitágoras no triângulo OMP: R² = (a/2)² + OM² -----> R² = 6² + [6.(2 + √3)]² = 36 + 144 + 108 + 144√3 = 288 + 144√3 ---->
-----> R² = 144.(2 + √3)
.:. R = 12.√(2 +√3) cm

trabalhando o radical duplo:
u² = 2² - (√3)² = 1 -----> u = 1

[latex]\\R = 12.\left[\sqrt{\frac{2+1}{2}}+\sqrt{\frac{2-1}{2}} \right ] = 12.\left(\frac{\sqrt{3}}{\sqrt{2}}+\frac{1}{\sqrt{2}} \right ) = 6\sqrt{2}.\left(\sqrt{3}+1 \right ) \\\\ \therefore\,\,\boxed{\,\,R = 6.\left(\sqrt{6}+\sqrt{2} \right )\,\,cm\,\,}[/latex]