Área do retângulo com geometria analítica

Os vértices de um retângulo no espaço estão sobre a reta r:(4,5,-1)+ [latex]\lambda [/latex](-2,1,2) e a reta s:x/4=(5-y)/2=(4-z)/4. Sabendo que o perímetro do retângulo é 6[latex]\sqrt{5}[/latex] escreva a área deste retângulo com duas casas decimais.

Os vértices A, B, C e D do retângulo estão sobre duas retas: r e s. Não sabemos se r e s contém as diagonais (fig. 1) ou lados opostos (fig. 2) do retângulo.


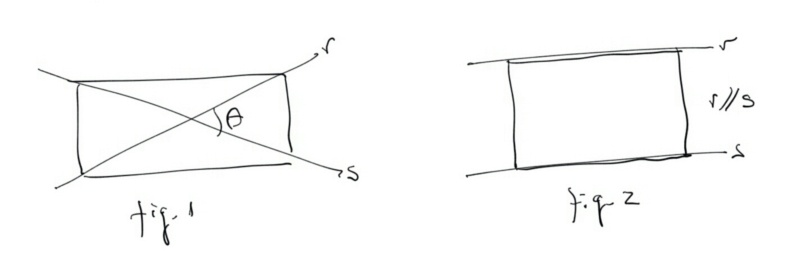
Sejam u e v os vetores diretores respectivamente a r e a s.
[latex]\\r:\ \left\{\begin{matrix} x=4-2\lambda\\y=5+\lambda \\z=-1+2\lambda \end{matrix}\right.\ \,\, \to\ \,\, \overrightarrow{u}=(-2, 1, 2)\ \to\ |\overrightarrow{u}|=3[/latex]
e
[latex]\\s:\ \frac{x}{4}=\frac{5-y}{2}=\frac{4-z}{4}\ \,\,\to\ \,\, \overrightarrow{v}=(4, -2, -4)\ \to\ |\overrightarrow{v}|=6[/latex]

Podemos perceber que o vetor v é conjugado linear do vetor u pois v = -2.u e portanto são paralelos. Logo r//s.
Se houver dúvida, calcule-se o ângulo \(\theta\) entre as retas:
\( cos\theta = \frac{\overrightarrow{u}\, .\,\overrightarrow{v}}{|\overrightarrow{u}| . |\overrightarrow{v}|} = \frac{-8-2+8}{3 . 6} = -1\,\, \rightarrow\,\,\theta=180º\,\,\Rightarrow\,\,r//s \)

Então estamos com o seguinte caso:


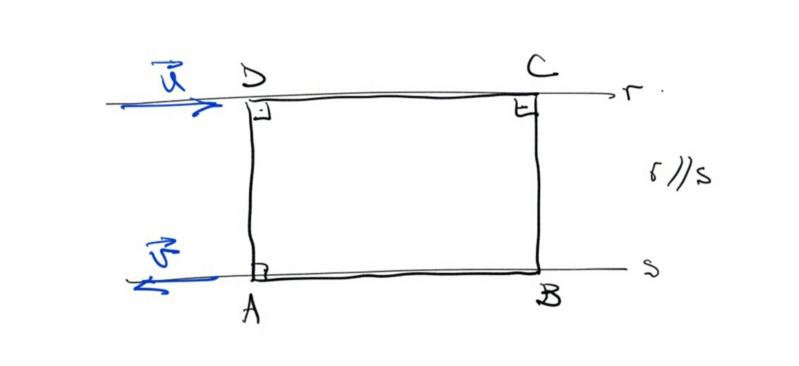
Do enunciado, perímetro \( 2p=6\sqrt{5}\ \rightarrow\ p=3\sqrt{5} \) , ou seja, \( AB+BC=3\sqrt{5} \).
Podemos calcular a distância entre as retas, ou seja, a medida de BC. Tomemos os pontos P(4, 5, -1), de r, e Q(0, 5, 4), de s; eles definem o vetor ligado \(\overrightarrow{w}\).

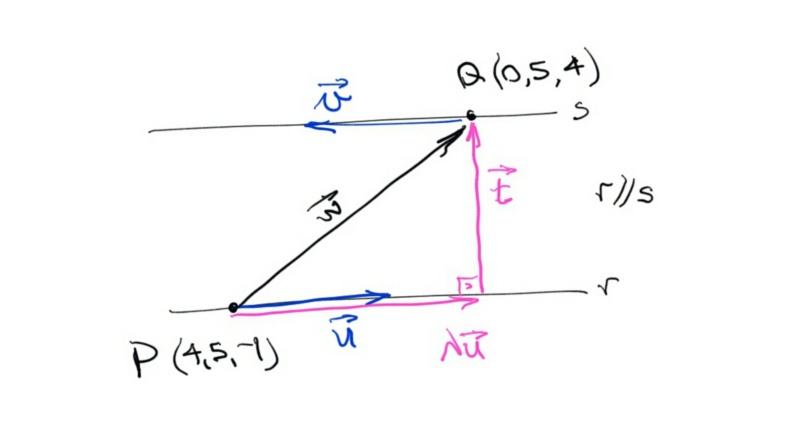
Nesta figura foi desenhado o vetor \(\overrightarrow{v}\) apenas para constar, ele não é necessário daqui em diante.