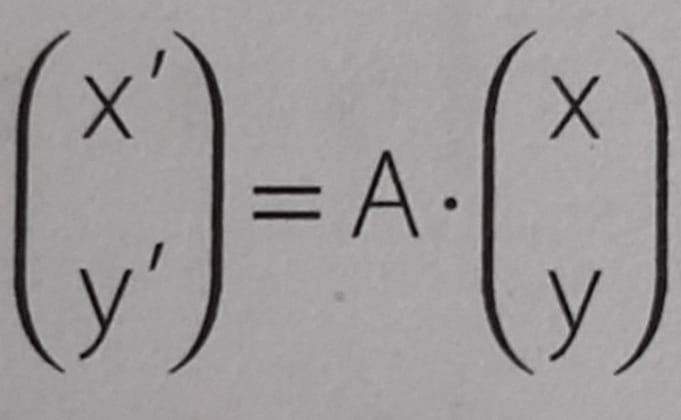Matrizes e Determinantes
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Re: Matrizes e Determinantes
Re: Matrizes e Determinantes
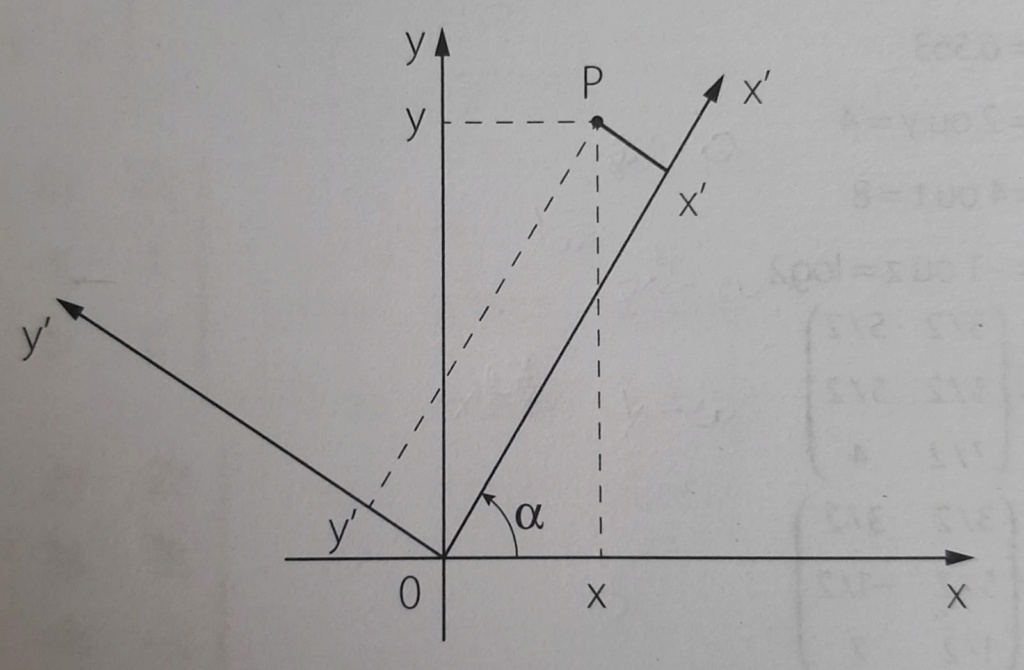
Seja Q a interseção do eixo x' com a reta vertical passando por P (em pontilhado na sua figura). Então
\(\cos \alpha= \dfrac{y'}{PQ} \implies PQ = \dfrac {y'}{ \cos \alpha}\)
Daí temos
\( \tan \alpha = \dfrac{y - PQ}{x} \implies x \sin \alpha = y \cos \alpha - PQ \cos \alpha = y \cos \alpha - y'\)
\( \boxed{ y' = -x \sin \alpha + y \cos \alpha}\)
Por outro lado, o segmento QO tem medida \(x' - PQ \sin\alpha\). Daí:
\(\cos \alpha = \dfrac{x}{QO} \implies x' \cos \alpha - PQ \sin \alpha \cos \alpha = x \implies \)
\( x = x' \cos \alpha - y' \sin \alpha = x' \cos\alpha - (-x \sin \alpha + y \cos \alpha) \sin \alpha \implies \)
\( x -x \sin^2 \alpha + y \cos \alpha \sin \alpha = x' \cos \alpha \implies \boxed{x' = x \cos \alpha + y \sin \alpha}\)
Organizando matricialmente temos:
\( \displaystyle
\left\{ \begin{array}{l}
x' = x \cos \alpha + y \sin \alpha\\
y' = -x \sin \alpha + y \cos \alpha
\end{array} \right. \implies
\begin{bmatrix}
x' \\ y'
\end{bmatrix} =
\begin{bmatrix}
\cos \alpha & \sin \alpha \\
- \sin \alpha & \cos \alpha
\end{bmatrix} \cdot
\begin{bmatrix}
x \\ y
\end{bmatrix} \)
\(\cos \alpha= \dfrac{y'}{PQ} \implies PQ = \dfrac {y'}{ \cos \alpha}\)
Daí temos
\( \tan \alpha = \dfrac{y - PQ}{x} \implies x \sin \alpha = y \cos \alpha - PQ \cos \alpha = y \cos \alpha - y'\)
\( \boxed{ y' = -x \sin \alpha + y \cos \alpha}\)
Por outro lado, o segmento QO tem medida \(x' - PQ \sin\alpha\). Daí:
\(\cos \alpha = \dfrac{x}{QO} \implies x' \cos \alpha - PQ \sin \alpha \cos \alpha = x \implies \)
\( x = x' \cos \alpha - y' \sin \alpha = x' \cos\alpha - (-x \sin \alpha + y \cos \alpha) \sin \alpha \implies \)
\( x -x \sin^2 \alpha + y \cos \alpha \sin \alpha = x' \cos \alpha \implies \boxed{x' = x \cos \alpha + y \sin \alpha}\)
Organizando matricialmente temos:
\( \displaystyle
\left\{ \begin{array}{l}
x' = x \cos \alpha + y \sin \alpha\\
y' = -x \sin \alpha + y \cos \alpha
\end{array} \right. \implies
\begin{bmatrix}
x' \\ y'
\end{bmatrix} =
\begin{bmatrix}
\cos \alpha & \sin \alpha \\
- \sin \alpha & \cos \alpha
\end{bmatrix} \cdot
\begin{bmatrix}
x \\ y
\end{bmatrix} \)

DaoSeek- Jedi

- Mensagens : 316
Data de inscrição : 29/07/2022
 Tópicos semelhantes
Tópicos semelhantes» Matrizes e Determinantes
» Matrizes e determinantes
» Determinantes de matrizes
» Matrizes e Determinantes
» Matrizes-Determinantes
» Matrizes e determinantes
» Determinantes de matrizes
» Matrizes e Determinantes
» Matrizes-Determinantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos