Geometria Plana - Morgado II

por giordanisuelen Qui 01 Set 2022, 19:49

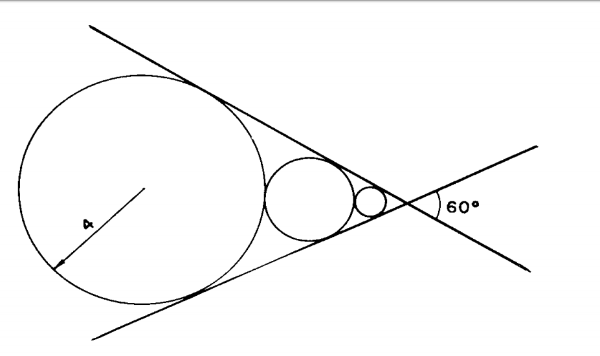
Considerando a figura abaixo, a soma dos diâmetros de todos os círculos é:

A)15
B)12
C)8
D)6
E)NRA.

Gabarito: B

Geometria Plana - Morgado II File

por Alien supremo Qui 01 Set 2022, 22:41

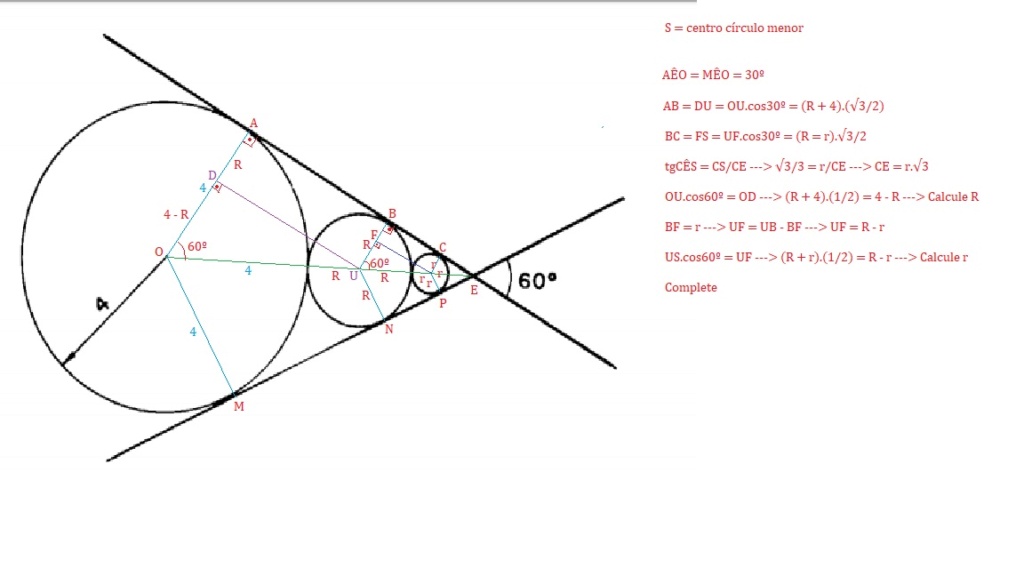
Cara, tenta fazer por geometria analítica. Escolhe o centro da circunferência maior para ser o centro do plano cartesiano. Com a construção de um triângulo retângulo com a circunferência maior você consegue descobrir os coeficientes angulares de ambas as retas. Depois você usa a fórmula da distância de um ponto a uma reta para descobrir cada raio de cada circunferência e, assim, soma todos os diâmetros.

por **Elcioschin** Qui 01 Set 2022, 23:39

por giordanisuelen Sex 02 Set 2022, 08:26

Obrigada!!!

por **Medeiros** Sáb 03 Set 2022, 23:44

outro modo.

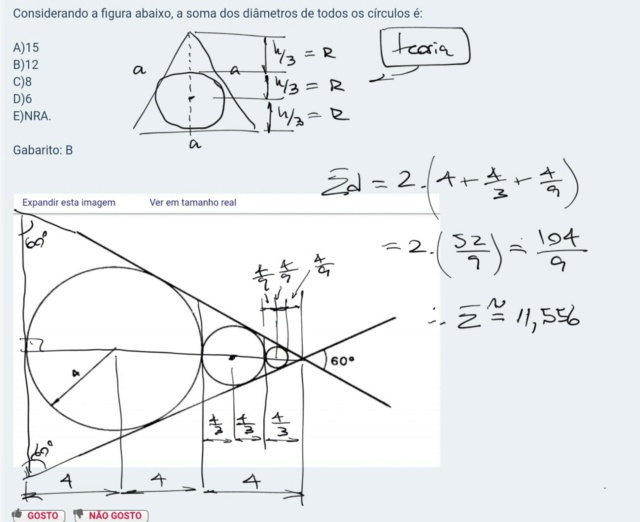
Sendo 60º o ângulo do vértice, o círculo de raio = 4 está inscrito num triângulo equilátero, caso em que o baricentro = incentro = ortocentro. Desta forma, o raio = 4 é 1/3 da altura do triângulo e os dois círculos menores ficam dentro dos 4 restantes da altura; então aplicamos novamente este raciocínio.

por giordanisuelen Dom 04 Set 2022, 14:43

Medeiros escreveu:outro modo.

Sendo 60º o ângulo do vértice, o círculo de raio = 4 está inscrito num triângulo equilátero, caso em que o baricentro = incentro = ortocentro. Desta forma, o raio = 4 é 1/3 da altura do triângulo e os dois círculos menores ficam dentro dos 4 restantes da altura; então aplicamos novamente este raciocínio.

Muito obrigada, Medeiros. Ótima resolução, me ajudou demais!!

por **Medeiros** Seg 05 Set 2022, 01:59

Observe que SE os círculos forem se reproduzindo infinitamente em direção ao vértice -- o que não está dito no enjunciado -- então a soma dos diâmetros seria o dado gabarito 12.

por **Elcioschin** Seg 05 Set 2022, 09:25

Concordo com o Medeiros: O enunciado está incompleto, pois a figura tem somente 3 círculos.

Se fosse uma questão de prova ou concurso, certamente teria sido anulada.

Uma explicação para a soma total ser 12:

S = 2.(4 + 4/3 + 4/9 + ......)

Temos uma PG infinita decrescente com a₁ = 4 e q = 1/3

S = 2[a₁/(1 - q)] ---> S = 2.[4/(1 - 1/3)] ---> S = 12