Baricentro

Na figura abaixo, tem-se um triângulo ABC. Sejam AA' = 9cm, BB' = 5cm, CC' = 7cm as distâncias dos vértices à reta r. Calcule a distância entre o baricentro O à mesma reta. 

gabarito:

Uma figura, para ajudar:

Por geometria analítica fica bastante fácil.

I) Coordenadas dos vértices:
A = (xa, 9)

B = (0, 5)

C = (xc, 7)

II) Coordenadas do baricentro:
G = (xa/3 + xb/3 + xc/3, ya/3 + yb/3 + yc/3)

Substituindo os valores:
G = (xa/3 + xc/3, 7)

A distância de G até a reta r é yG = 7 cm.

Vou deixar o roteiro para você resolver por geometria plana e ver a trabalheira comparada com a geometria analítica.

I) Tome o ponto médio de BC.

II) No trapézio BB'C'C construa a base média, ela medirá 6 cm.

III) Tome o ponto médio de AC.

IV) No trapézio AA'C'C construa a base média, ela medirá 8 cm.

V) Tome o ponto de encontro entre as medianas pelos vértices A e B do triângulo ABC (é o baricentro).

VI) Tome o ponto que divide a mediana por B em 3 partes iguais (lembre-se que o baricentro divide a mediana na razão 2:1).

VII) Construa a base média do trapézio que passa pelo ponto anterior. Chamanado a sua medida de x, temos que esta medida é base média de um trapézio (identifique), logo:
x = (y + 5)/2 em que y é a medida procurada.

Por outro lado, y também é base média de um trapézio (identifique), logo:
y = (x + /2

Resolvendo o sistema obtemos y = 7 cm.

Caso você não entenda alguma passagem pode me comunicar.

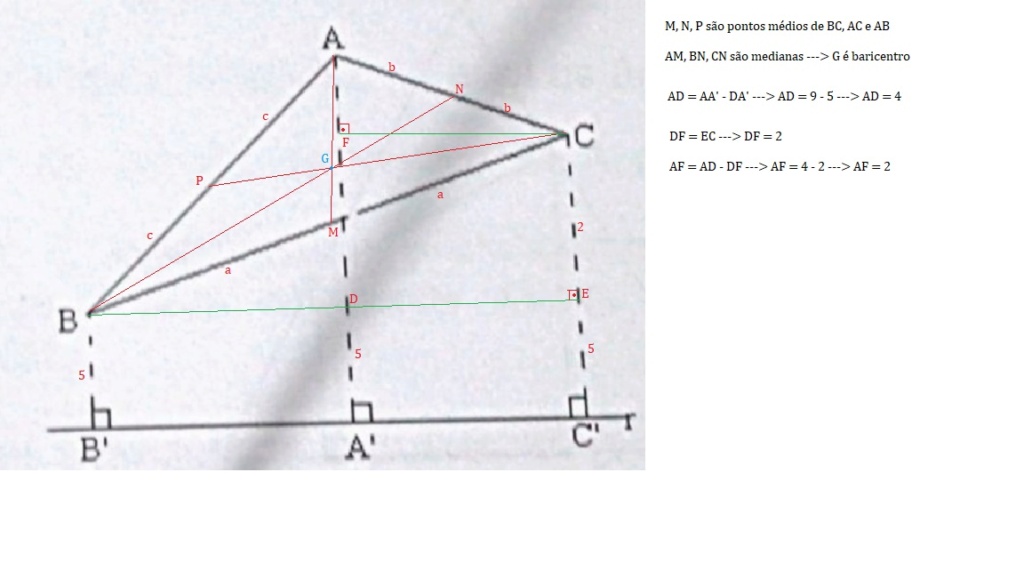
Seja Q o ponto na reta AA' tal que QAB é um triângulo retângulo. Desse modo, QA = 9 - 5 = 4.

Se P é o ponto médio de AB, então AP = PB. Dado o ponto R em BQ tal que RPB, podemos concluir, por semelhança, que RP = QA/2 = 2, já que PB = AB/2. 

Assim, tendo em vista que a "altura" de P até o chão é 5+2 = 7, concluímos que PCC' é um ângulo reto.  Portanto, a altura o baricentro é igual a 7 cm, já que todos os pontos da reta PC têm a mesma altura, e o baricentro é um deles.

Será que o meu raciocínio tá certo?

É verdade, nesse caso, mas se trocássemos a medida de CC' para 8 cm, a resposta (ao que me parece) já não seria simples assim.
 
Boa solução, btw!

mesma questão com outros valores
https://pir2.forumeiros.com/t168651-geometria-plana-triangulos

uma questão parecida
https://pir2.forumeiros.com/t3870-triangulo-inclinado-em-relacao-a-um-plano

Muitíssimo grato pela ajuda, colegas. Compreendi perfeitamente. 

Rory Gilmore escreveu:É verdade, nesse caso, mas se trocássemos a medida de CC' para 8 cm, a resposta (ao que me parece) já não seria simples assim.
 
Boa solução, btw!

Sim, eu concordo totalmente! Seria bem complicado fazer por geometria plana se CC' fosse diferente da média de AA' e BB'.  Por isso eu prefiro a sua solução por geometria analítica, é realmente bem mais fácil e vale pra todos os casos.