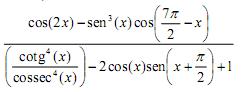Equação trigonométrica
2 participantes
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
 Equação trigonométrica
Equação trigonométrica
Última edição por samuelbelembr@gmail.com em Qui 05 maio 2022, 11:01, editado 1 vez(es)
samuelbelembr@gmail.com- Jedi

- Mensagens : 205
Data de inscrição : 04/10/2021
 Re: EQUAÇÃO TRIGONOMÉTRICA
Re: EQUAÇÃO TRIGONOMÉTRICA
Fala, Samuel.
[latex]\frac{cos(2x)-sen^3(x)cos(\frac{7\pi}{2}-x)}{(\frac{cotg^4(x)}{cossec^4(x)})-2cos(x)sen(x+\frac{\pi}{2})+1}[/latex]
[latex]\frac{cos(2x)+sen^4(x)}{cos^4(x)-2cos^2(x)+1}[/latex]
[latex]\frac{1-2sen^2(x)+sen^4(x)}{cos^4(x)-2cos^2(x)+1}[/latex]
Olha o produto notável na forma (a-b)^2 = a^2 - 2ab + b^2:
[latex]\frac{(sen^2(x)-1)^2}{(cos^2(x)-1)^2}[/latex]
[latex]\frac{(1-cos^2(x)-1)^2}{(1-sen^2(x)-1)^2} = \frac{cos^4(x)}{sen^4(x)} = cotg^4(x)[/latex]
[latex]\frac{cos(2x)-sen^3(x)cos(\frac{7\pi}{2}-x)}{(\frac{cotg^4(x)}{cossec^4(x)})-2cos(x)sen(x+\frac{\pi}{2})+1}[/latex]
[latex]\frac{cos(2x)+sen^4(x)}{cos^4(x)-2cos^2(x)+1}[/latex]
[latex]\frac{1-2sen^2(x)+sen^4(x)}{cos^4(x)-2cos^2(x)+1}[/latex]
Olha o produto notável na forma (a-b)^2 = a^2 - 2ab + b^2:
[latex]\frac{(sen^2(x)-1)^2}{(cos^2(x)-1)^2}[/latex]
[latex]\frac{(1-cos^2(x)-1)^2}{(1-sen^2(x)-1)^2} = \frac{cos^4(x)}{sen^4(x)} = cotg^4(x)[/latex]
João Pedro Lima- Jedi

- Mensagens : 220
Data de inscrição : 02/01/2022
Idade : 22
Localização : Rio de Janeiro, RJ
 Tópicos semelhantes
Tópicos semelhantes» Equação trigonométrica - Equação simples
» Equação Trigonométrica
» equação trigonométrica
» Equação Trigonométrica
» Equação trigonométrica
» Equação Trigonométrica
» equação trigonométrica
» Equação Trigonométrica
» Equação trigonométrica
PiR2 :: Matemática :: Trigonometria
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos