Pré-Cálculo
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Pré-Cálculo
por Convidado Qui 03 Mar 2022, 14:11
o polinômio p(x)= - 12x4 + 4x3 + 9x2 +1
a) Quais são as possíveis raízes racionais não inteiras de p(x)? Justifique sua resposta.
b) Sabendo que o polinômio p(x) possui apenas uma raiz inteira, determine essa raiz inteira.
Se x = x1 é a raiz inteira, obtenha o polinômio q(x) que satisfaz p(x) = -12x4 + 4x3 + 9x2 - 6x = (x - x1) q(x)
a) Quais são as possíveis raízes racionais não inteiras de p(x)? Justifique sua resposta.
b) Sabendo que o polinômio p(x) possui apenas uma raiz inteira, determine essa raiz inteira.
Se x = x1 é a raiz inteira, obtenha o polinômio q(x) que satisfaz p(x) = -12x4 + 4x3 + 9x2 - 6x = (x - x1) q(x)
Última edição por lalimina em Qui 03 Mar 2022, 21:47, editado 5 vez(es)
Convidado- Convidado
Re: Pré-Cálculo
por qedpetrich Qui 03 Mar 2022, 14:13
lalimina escreveu:????(????) = −12????4 + 4????3 + 9????2 − 6???? + 1
a)Quais são as possíveis raízes racionais não inteiras de ????(????)? Justifique sua resposta.
b)Sabendo que o polinômio ????(????) possui apenas uma raiz inteira, determine essa raiz inteira.
c)Se ???? = ????1 é a raiz inteira, obtenha o polinômio ????(????) que satisfaz ????(????) = −12????4 + 4????3 + 9????2 − 6???? + 1 = (???? − ????1) ????(????).
d)Determine as raízes racionais não inteiras do polinômio ????(????) encontrado no item Q3(b) e fatore ????(????).
O que significa ????, por favor [EDIT] sua postagem.
____________________________________________
Dê tempo ao
Lateralus Φ
qedpetrich- Monitor
- Mensagens : 2498
Data de inscrição : 05/07/2021
Idade : 24
Localização : Erechim - RS / Passo Fundo - RS
aitchrpi gosta desta mensagem
Re: Pré-Cálculo
por qedpetrich Qui 03 Mar 2022, 14:34
Perceba que p(-1) = 0, logo, aplicando o dispositivo de Briot-Ruffini:
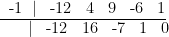
Assim: z(x) = -12x³ + 16x² - 7x + 1, novamente note que z(1/2) = 0, aplicando novamente a mesma ideia:
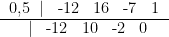
Logo: t(x) = -12x² + 10x - 2 = 0
Acho que a partir daqui você consegue prosseguir, lembre-se que se as raízes de t(x) e z(x) também são raízes de p(x). Se ainda não conseguir desenvolver, mande suas dúvidas.
OBS: Você postou na categoria errada, não têm nada a ver com Geometria Analítica. Atente-se nas próximas postagens.
Assim: z(x) = -12x³ + 16x² - 7x + 1, novamente note que z(1/2) = 0, aplicando novamente a mesma ideia:
Logo: t(x) = -12x² + 10x - 2 = 0
Acho que a partir daqui você consegue prosseguir, lembre-se que se as raízes de t(x) e z(x) também são raízes de p(x). Se ainda não conseguir desenvolver, mande suas dúvidas.
OBS: Você postou na categoria errada, não têm nada a ver com Geometria Analítica. Atente-se nas próximas postagens.
____________________________________________
Dê tempo ao
Lateralus Φ
qedpetrich- Monitor
- Mensagens : 2498
Data de inscrição : 05/07/2021
Idade : 24
Localização : Erechim - RS / Passo Fundo - RS
aitchrpi gosta desta mensagem
Re: Pré-Cálculo
por qedpetrich Qui 03 Mar 2022, 19:33
Lalimina, gostaria de entender o motivo de você remover o enunciado da questão, vou pedir encarecidamente que você restitua o mesmo. Segundo o regulamento do fórum PiR²:
VI- Deve-se postar apenas uma questão por tópico, um tópico para cada questão. Uma vez que uma questão obtiver uma resposta ela passará a ser de domínio público não podendo o usuário autor da questão modificá-la ou deletá-la, consistindo esse ato em infração.
Acredito que ficou bem claro quando o Euclides escreveu.
VI- Deve-se postar apenas uma questão por tópico, um tópico para cada questão. Uma vez que uma questão obtiver uma resposta ela passará a ser de domínio público não podendo o usuário autor da questão modificá-la ou deletá-la, consistindo esse ato em infração.
Acredito que ficou bem claro quando o Euclides escreveu.
____________________________________________
Dê tempo ao
Lateralus Φ
qedpetrich- Monitor
- Mensagens : 2498
Data de inscrição : 05/07/2021
Idade : 24
Localização : Erechim - RS / Passo Fundo - RS
aitchrpi gosta desta mensagem
Tópicos semelhantes» Cálculo Integral - Problema envolvendo cálculo de área
» Cálculo
» Cálculo 2: Cálculo de Volumes
» Cálculo I
» Cálculo de Nox
» Cálculo
» Cálculo 2: Cálculo de Volumes
» Cálculo I
» Cálculo de Nox
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
