Inversa de função composta
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Inversa de função composta
por gabiicrisgc@ Qua 02 Fev 2022, 15:54
Sejam os conjuntos A = {x ∈ ℝ l x ≥ -2}, B = {x ∈ ℝ l x ≥ - 4} e C = {x ∈ ℝ l x ≥ -1} e as funções f de A em B definida por f(x) = x² + 4x e g de B em C definida por g(x) = x² - 1. Pergunta-se: existe g(f(x))-1? Justificar a resposta.
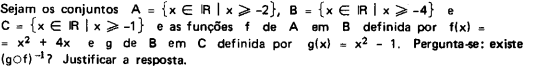
Alguem pode me ajudar? ja tentei fazer mas nao deu certo. Me ajudee!!!!!!!!
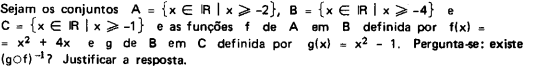
Alguem pode me ajudar? ja tentei fazer mas nao deu certo. Me ajudee!!!!!!!!
gabiicrisgc@- Iniciante
- Mensagens : 2
Data de inscrição : 02/02/2022
Re: Inversa de função composta
por Rory Gilmore Qua 02 Fev 2022, 16:32
Olá, bem-vinda!
Não existe inversa de g(f(x)) porque g não é inversível. A composta só é inversível se ambas forem inversíveis.
Para provar que g não é inversível basta construir o seu gráfico e ver que ela não é injetora em [-4, +∞[
OBS: eu tive que editar sua mensagem porque você não digitou a questão e colocou o título em maiúsculas. Nas próximas postagens sempre escreva a questão e informe o gabarito se souber.
Não existe inversa de g(f(x)) porque g não é inversível. A composta só é inversível se ambas forem inversíveis.
Para provar que g não é inversível basta construir o seu gráfico e ver que ela não é injetora em [-4, +∞[
OBS: eu tive que editar sua mensagem porque você não digitou a questão e colocou o título em maiúsculas. Nas próximas postagens sempre escreva a questão e informe o gabarito se souber.
Rory Gilmore- Monitor
- Mensagens : 1878
Data de inscrição : 28/05/2019
Localização : Yale University - New Haven, Connecticut
gabiicrisgc@ gosta desta mensagem
Re: Inversa de função composta
por gabiicrisgc@ Sex 04 Fev 2022, 14:53
Obrigada pela ajuda!
Desculpe pelo erro.
Desculpe pelo erro.
gabiicrisgc@- Iniciante
- Mensagens : 2
Data de inscrição : 02/02/2022
Rory Gilmore gosta desta mensagem
Tópicos semelhantes» Função composta e inversa
» função inversa e composta
» Função Composta e Inversa
» Função composta e inversa
» Função composta e inversa
» função inversa e composta
» Função Composta e Inversa
» Função composta e inversa
» Função composta e inversa
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
