Geometria Espacial

Mostre que os seis planos mediadores das arestas de um tetraedro passam por um mesmo ponto que é equidistante dos quatro vértices.

Boa tarde!
Exercício bem complicado, mas extremamente interessante. Vou mostrar como consegui desenvolver. 
(Observação: representarei o segmento de uma reta entre colchetes; veja "[AB]" como "o segmento de reta AB")

Talvez a primeira dúvida que possa aparecer seja: o que são planos mediadores? Resumidamente, um plano mediador é um plano no espaço que intercepta, perpendicularmente, um segmento de reta em seu ponto médio. Caso ainda reste dúvidas, veja esse site: http://lugaresgeometricos.weebly.com/plano-mediador.html

Familiarizados com o conceito, o exercício quer que nós mostremos que os planos mediadores das arestas passam pelo ponto equidistante dos vértices do tetraedro. Minha estratégia é que, primeiramente, entendamos qual é esse ponto equidistante para que, posteriormente, consigamos mostrar o que nos é pedido.


Observe a figura abaixo que desenhei:



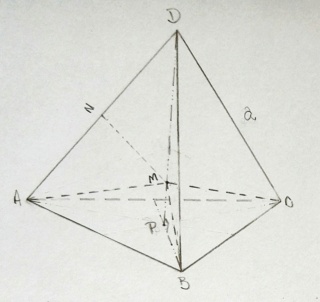
Tome, primeiramente, o triângulo ABC. Como as arestas do tetraedro são todas iguais, ΔABC é equilátero. Sabe-se que o ponto equidistante dos vértices de um triângulo é seu circuncentro. Além disso, em um triângulo equilátero, circuncentro, baricentro, incentro e ortocentro coincidem. Assim, descobrindo-se o baricentro de ΔABC, descobre-se, também, seu circuncentro. Chame o baricentro de ΔABC de P. Note que o lugar geométrico equidistante de A, B e C é, justamente, a reta perpendicular ao plano de ΔABC, passando por P. Como [AD] = [BD] = [CD], então essa reta também passa por D, de sorte que [PD] faz parte do lugar geométrico equidistante de A, B e C. Daí, o ponto equidistante de A, B, C, e D será um ponto M, pertencente a [PD], tal que [MA] = [MD].

Perceba agora, que, os planos mediadores das arestas [AB], [BC] e [CA] coincidem com as alturas de ΔABC. Caso isso não seja tão claro, peguemos, por exemplo, [AB]. Veja que o plano mediador de [AB] é perpendicular ao segmento e passa pelo ponto médio. A altura relativa a [AB], por sua vez, também é perpendicular ao segmento e, por se tratar de um triângulo equilátero, passará pelo ponto médio de [AB]. Conseguiu perceber a semelhança entre os dois? Se ainda houver dúvidas com relação a isso, tente desenhar a figura esboçando os planos mediadores.

Ótimo, agora que conseguimos notar isso, podemos concluir que os planos mediadores das arestas [AB], [BC] e [CA] se interceptam em [PD]. Com isso em mente, já sabemos que esses planos mediadores interceptam o ponto M, equidistante dos vértices, já que esse pertence a [PD]. Basta agora, que verifiquemos se os planos mediadores de [AD], [BD] e [CD] também interceptam M.

Veja, na figura, o ponto M. Perceba que, se M é equidistante dos vértices, então [MA] = [MD], de sorte que ΔAMD é isósceles. Sabendo-se que o ponto N é o ponto médio de [AD], como o triângulo é isósceles, a altura relativa ao lado de medida diferente é perpendicular e passa pelo ponto médio desse lado, o ponto N. Note, novamente, a semelhança dessa altura com o plano mediador de [AD]. De fato, esse irá se comportar como os outros planos que analisamos: pode ser visto como um "prolongamento vertical" da altura relativa. Pela simetria da figura, o mesmo ocorrerá para os planos mediadores de [BD] e [CD]. 

Perceba que os planos mediadores de [AD], [BD] e [CD] se interceptam em uma reta que passa por M e é perpendicular a [PD]. É difícil visualizar isso sem desenhar, se facilitar, desenhe. Ora, duas retas perpendiculares se encontram apenas em um ponto. Se os planos mediadores de [AB], [BC] e [CA] se interceptam em [PD] e os planos de [AD], [BD] e [CD] se interceptam em uma reta perpendicular a [PD], há apenas um ponto de encontro: M. 

Pronto, mostramos que os planos mediadores das arestas passam por um mesmo ponto que é equidistante dos quatro vértices do tetraedro. É claro, tentei desenvolver uma demonstração mais qualitativa do exercício, você poderia seguir uma ideia mais quantitativa. 

Caso se interesse pela solução mais quantitativa, você poderia prosseguir da seguinte forma:

Analise o baricentro de ΔABC, lembrando-se que ele divide as alturas na razão 1:2. Descubra o valor de [PB] utilizando a altura de ΔABC. Analise, posteriormente, ΔPBD, aplicando Pitágoras e descubra [PD]. Daí, analise ΔPMA. Aplique Pitágoras, notando que [PA] = [PB] e [PM] = [PD] - [MD], e descubra [MD]. Utilize [PM] = [PD] - [MD] e descubra [PM]. O fato de existir um valor para M prova que existe um ponto equidistante dos vértices. Por fim, prove que esse ponto também é equidistante das arestas e, conclua a partir daí, que os planos mediadores interceptam M. 

É um pouco mais trabalhoso e, dependendo do seus objetivos com estudo de geometria espacial, talvez não seja tão interessante despender muito tempo nisso. 

No mais, é isso. Se houver qualquer dúvida em relação ao meu desenho ou algum erro de digitação, me avise.