Máximo e mínimo da função

Boa tarde prezados usuários do Pir²!
Encontre os valores máximo e mínimo da função , com .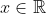 
Peço por gentileza que detalhe o máximo a resolução. Tenho muita dificuldade e estudo pelas resoluções que apresentam. 
Pietro

Boa tarde!
Nesse tipo de exercício é importante que entendamos um pouco sobre a análise dos gráficos das funções trigonométricas. 
Primeiramente, vamos tentar reduzir a função dada a apenas uma função trigonométrica, ou seja, deixar apenas em função de seno, ou apenas em função de cosseno. Vou escolher cosseno, mas ressalto que ambas as escolhas proveriam os mesmos resultados.
Convido-o a lembrar-se da relação fundamental: sen²(x) + cos²(x) = 1. Isolando-se sen²(x), vem: sen²(x) = 1 -cos²(x). Legal, conseguimos definir o quadrado do cosseno a partir do quadrado do seno, vamos substituir essa informação na função, veja:

h(x) = 7sen²(x) + 11cos²(x) ⇒ h(x) = 7[1 - cos²(x)] + 11cos²(x) ⇒ h(x) = 4cos²(x) + 7.

Ótimo, conseguimos deixar em função apenas de cosseno. Isso é importante porque a análise se torna mais fácil quando há apenas um parâmetro a ser analisado. Caso tivéssemos duas funções trigonométricas distintas, elas teriam propriedades diferentes e, consequentemente, seria mais trabalhoso identificar os pontos de máxima e mínima. 

Bom, agora entra, de fato, a parte que comentei sobre os gráficos das funções. Lembra-se dos pontos de máxima e mínima da função cosseno? A função cosseno assume valor máximo para 2kπ, k ∈ Z, tendo seu valor igual a 1. Em contrapartida, essa assume valor mínimo para π + 2kπ, k ∈ Z, tendo seu valor igual a -1. 

Essa análise é importante, mas não ajuda a solucionar totalmente o exercício. Veja que na função que conseguimos estabelecer, a função cosseno está ao quadrado, de forma que valores negativos não aparecerão. Dessa forma, não podemos assumir que o valor mínimo de cos²(x) é -1. Caso isso não seja claro, imagine cos²(x) como [cos(x)]². Substitua, agora, x por π. Veja que teríamos [cos(π)]² = (-1)² = 1. Percebeu que, para x = π, enquanto cos(x) assume valor mínimo, cos²(x) assume valor máximo? 

Nesse caso, como descobrir o valor mínimo de cos²(x)? 

Há duas maneiras habituais. A primeira seria vendo o gráfico da função, o qual lhe convido a, posteriormente, dar uma olhada. A segunda seria percebendo que, como cos²(x) não assume valores negativos, o menor valor que ele poderá assumir é 0.

Em posse disso, podemos sintetizar que: máx cos²(x) = 1 e mín cos²(x) = 0.

Com isso, basta substituir na função que estabelecemos, veja:

Para o valor máximo: h(x) = 4 . 1 + 7 = 11

Para o valor mínimo: h(x) = 4 . 0 + 7 = 7


Deixo como complemento, o gráfico da função inicialmente dada. Perceba que os pontos de máxima e mínima condizem com o que foi analisado. 
https://i.servimg.com/u/f64/20/39/96/55/imagem10.png

Muitíssimo obrigado, amigo.
Muito bem detalhada a sua resolução.