Geometria Espacial

Seja P um ponto exterior a um plano π. Para cada ponto Q de π seja X o ponto do segmento P Q que o divide na razão d(X,P)/d(X, Q) = k

Qual é o lugar geométrico do ponto X quando Q percorre o plano π.

Tomemos Q como projeção de P sobre π. E vamos inicialmente considerar apenas uma reta r de π passando por Q. O ponto X divide PQ nos segmentos a e b (vide desenho); assim escrevemos a razão k = a/b.
Com um outro ponto Q₁ sobre r temos o segmento PQ₁ e o ponto X₁ mantendo a mesma razão k = a₁/b₁. Podemos estender essa mecânica para os infinitos pontos de r mas basta-nos analisar estes dois (Q e Q₁)



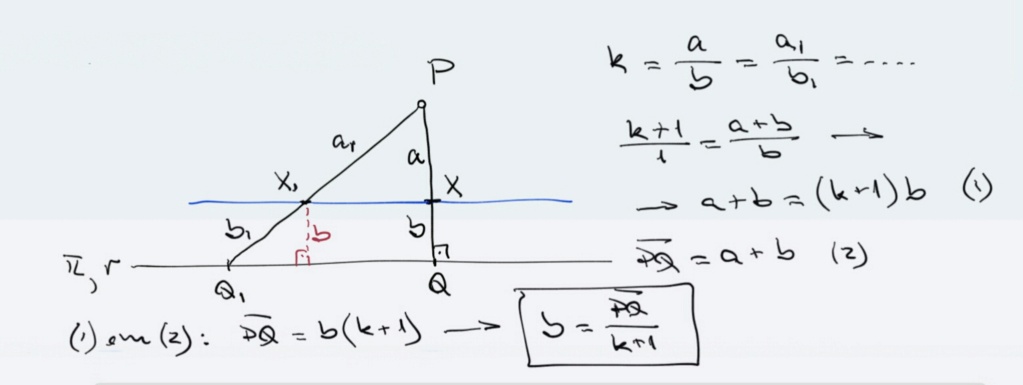
Como k = a/b = a₁/b₁ = .... , por Tales podemos concluir que a reta suporte do segmento XX₁ é paralela à reta r, portanto paralela ao plano π. Ainda, que a distância desta reta ao plano π mede b.

Considere agora as infinitas retas de π que são concorrentes em Q; com isto abarcamos TODOS os pontos do plano π. Podemos estender o raciocínio acima para todas essas retas e obteremos o mesmo resultado: os infinitos pontos X distarão a medida b do plano π. Portanto o lugar geométrico do ponto X quando Q percorre o plano π é um plano paralelo a π, entre π e P, à distância b de π, onde
as contas para chegar neste resultado estão na figura acima.