Questão da UFRS

por Pierre Dzurunda Seg 13 Set 2021, 12:00

Observe a figura abaixo, onde o ponto inicial da poligonal representada é a origem do sistema de coordenadas. Os comprimentos dos lados dessa poligonal formam a sequência 1, 1, 2, 2, 3, 3, 4, 4, 5, 5.

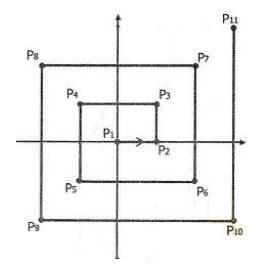
Considerando que a poligonal continue evoluindo de acordo com o padrão acima apresentado, o primeiro ponto do 50° lado é:
a) (-13, -13)
b) (-13, 13)
c) (12,-12)
d) (13, -12)
e) (13, -13)

Spoiler:

por eivitordias Seg 13 Set 2021, 19:47

Olá, @Pierre Dzurunda.

Vamos ordenar alguns pontos:

(0,0), (1,0), (1,1), (-1,1), (-1,-1), (2,-1), (2,2), (-2,2), (-2,-2), (3,-2), ...

Perceba que a partir de P3 temos uma sequência lógica, em blocos de 4 coordenadas, sendo x correspondente ao bloco analisado (azul bloco 1 --> x=1, rosa bloco 2 --> x=2, ...).

A sequência em cada bloco é:

1) x=y;
2) (-x, y);
3) (-x, -y);
4) (x+1, -y).

Desprezando P1 e P2, para obter as coordenadas do 50º termo:

48/4 = 12 blocos

Desse modo, percebe-se que o 50º termo é a ultima coordenada do 12º bloco ---> x=12.

Logo: ---> (x+1, -y) ---> (13, -12).

Questão da UFRS

Questão da UFRS

Re: Questão da UFRS

Um fórum livre e democrático.