Números Complexos
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Números Complexos
Números Complexos
Represente no plano de Argand-Gauss o lugar geométrico das imagens dos números complexos z, tais que:
|z+3|+|z-3|=10
O gabarito diz que é uma elipse de equação x²/25 + y²/16 = 1, porém só consigo encontrar uma circunferência.
|z+3|+|z-3|=10
O gabarito diz que é uma elipse de equação x²/25 + y²/16 = 1, porém só consigo encontrar uma circunferência.
Última edição por igorsalves em Sex Ago 20 2021, 18:12, editado 1 vez(es)
igorsalves- Iniciante
- Mensagens : 2
Data de inscrição : 20/08/2021
Idade : 22
Localização : Porto Alegre-RS
 Re: Números Complexos
Re: Números Complexos
Fala, meu consagrado! Tudo Certo?
Um jeito de você bater o olho na expressão e falar: "Ah! É uma elipse!" ou "Ah! É uma circunferência!" é o seguinte:
1⁰)Qual é a principal propriedade da circunferência?
É a distância de um ponto sendo uma constante, ou seja, a equação geral de uma circunferência no Plano de Argand-Gauss é:

2⁰)Qual é uma das principais características da elipse?
É soma de duas distâncias dando o 2.a, que é uma constante, certo?
De tal forma, observe que para a expressão de uma elipse, no plano de Argande-Gauss, a soma de duas distâncias é uma constante. Coincidência?! NÃO!
Desse modo, conseguimos extrair, da expressão dada, o "a" e o "c"

Observe que os focos estão nos pontos (3,0) e (-3,0), de tal forma que a distância entre eles é o eixo focal, ou seja, 2.c=6-----> c=3 e 10 é o eixo maior, ou seja, 2.a=10----> a=5.
Assim, podemos aplicar aquele "Pitágoras da elipse":

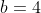
De tal forma, conseguimos a seguinte equação da elipse:
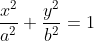

Espero ter ajudado! Grande Abraço!
Um jeito de você bater o olho na expressão e falar: "Ah! É uma elipse!" ou "Ah! É uma circunferência!" é o seguinte:
1⁰)Qual é a principal propriedade da circunferência?
É a distância de um ponto sendo uma constante, ou seja, a equação geral de uma circunferência no Plano de Argand-Gauss é:
2⁰)Qual é uma das principais características da elipse?
É soma de duas distâncias dando o 2.a, que é uma constante, certo?
De tal forma, observe que para a expressão de uma elipse, no plano de Argande-Gauss, a soma de duas distâncias é uma constante. Coincidência?! NÃO!
Desse modo, conseguimos extrair, da expressão dada, o "a" e o "c"
Observe que os focos estão nos pontos (3,0) e (-3,0), de tal forma que a distância entre eles é o eixo focal, ou seja, 2.c=6-----> c=3 e 10 é o eixo maior, ou seja, 2.a=10----> a=5.
Assim, podemos aplicar aquele "Pitágoras da elipse":
De tal forma, conseguimos a seguinte equação da elipse:
Espero ter ajudado! Grande Abraço!

FocoNoIMEITA- Jedi

- Mensagens : 270
Data de inscrição : 05/05/2020
Idade : 22
Localização : Rio de Janeiro-RJ
igorsalves gosta desta mensagem
 Re: Números Complexos
Re: Números Complexos
Feito irmão, fez sentido, obrigado!
igorsalves- Iniciante
- Mensagens : 2
Data de inscrição : 20/08/2021
Idade : 22
Localização : Porto Alegre-RS
FocoNoIMEITA gosta desta mensagem
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos













