arcos em uma semicircunferência

por pedrohadc Qui 22 Abr 2021, 17:20

A figura a seguir apresenta uma semicircunferência de diâmetro -AB, com raio igual a 3cm e com o ponto C sobre a semicircunferência.

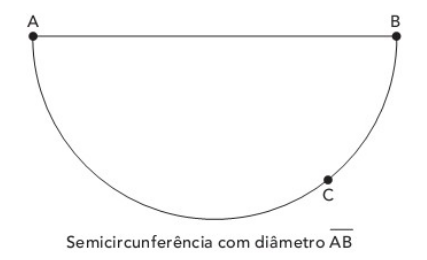
Sabendo que o segmento -AC mede 3cm, qual é o comprimento do arco ~AC?
a) 3pi((sqrt3)/2)cm
b) pi((sqrt3)/3)cm
c) 4pi((sqrt3)/3)cm
d) 2pi((sqrt3)/3)cm
e) 3picm

gabarito:

no triângulo ABC, o ângulo ^C está associado ao arco AB (que vale 180°), então ele deve valer 90°
pois, como é um triângulo retângulo:
sin(^B) = -AC/-AB
sin(^B) = 3cm/6cm
sin(^B) = sind(30)
^B = 30°
como o ângulo ^B está associado ao arco ~AC:
^B = ~AC/2
~AC = 60°
o comprimento da circunferência (360°) é
C = 6picm
já que ~AC é 1/6 da circunferência:
Cac = 6picm/6
Cac = picm
onde estou errando?

por **SilverBladeII** Qui 22 Abr 2021, 18:56

Uma outra sol: Se O é o centro, AC=AO=CO e portanto AOC é equilatero e então AOC=60º=pi/3 rad, de forma que AC=r*pi/3=pi.
Mesmo resultado que vc chegou.

Pode ter um erro no enunciado ou nas alternativas, talvez?