Calcule a área do trapézio . (UNICHRISTUS/2017.2)

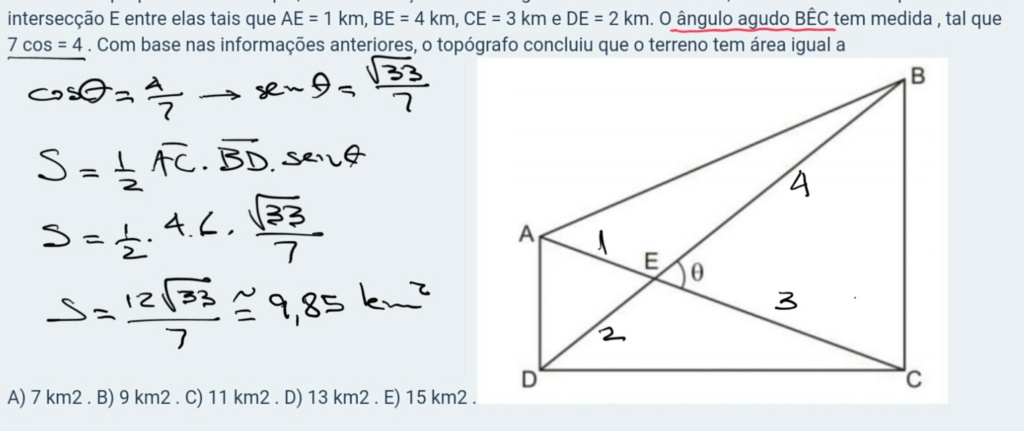
Visando a obter uma informação precisa de sua nova fazenda, Sr. Anastácio contratou um topógrafo para que pudesse saber, com precisão, a área do terreno de sua fazenda. Para facilitar os trabalhos, o topógrafo responsável decidiu utilizar uma vista aérea do terreno por meio de uma foto via satélite. O terreno tem o formato de um quadrilátero ABCD. A escritura da propriedade relata que, se forem traçados dois segmentos de reta AC e BD, encontraremos um ponto de intersecção E entre elas tais que AE = 1 km, BE = 4 km, CE = 3 km e DE = 2 km. O ângulo agudo BÊC tem medida , tal que cos = [7^(1/2)]/4 . Com base nas informações anteriores, o topógrafo concluiu que o terreno tem área igual a 
A) 7 km2 . B) 9 km2 . C) 11 km2 . D) 13 km2 . E) 15 km2 .

RESPOSTA: LETRA b

AÊD = BÊC = θ ---> cosθ = √7/4 ---> cos²θ = 7/16 ---> sen²θ = 9/16 ---> senθ = 3/4

S = x.y.senθ/2


S1 = 1.2.(3/4)/2 ---> S1 = 3/4
S2 = 1.4.(3/4)/2 ---> S2 = 6/4
S3 = 2.3.(3/4)/2 ---> S3 = 18/4
S4 = 3.2.(3/4)/2 ---> S1 = 9/4

S = S1 + S2 + S3 + S4 ---> S = 9

Outro modo.

prezado Dieg

1)
vc alterou a questão depois das respostas dadas -- e não indicou (realçou) as alterações! Eu é que não vou procurar onde ocorreu alteração e nem refazer contas. Então, agora, faça vc as contas, verifique se confere o gabarito e mostre-as para todos.

2)
talvez sintam falta, na minha resolução anterior, da demonstração do porquê pode ser feita aquele tipo de conta. Então segue:

a área de um quadrilátero convexo qualquer é a mesma do triângulo formado com suas diagnonais e mesmo ângulo entre elas.

prolongamos BC de um comprimento DF igual AD. Traçamos DF paralelo a AD. Então BˆDF = BÊC = θ. Por construção os triângulos ABD e CDF têm áreas iguais. A área do triângulo BCD é comum ao quadrilátero e ao triângulo. Portanto a área do quadrilátero ABCD é igual à do triângulo BDF.

A região é formada por 4 triângulos cujos lados são todos dados. Agora, tendo em mente que a área de um único triângulo, por resultados da geometria analítica, é dado sempre pelo produto dos lados vezes o seno do ângulo entre eles dividido por 2, obtemos as quatro áreas dos quatro triângulos que dividem a figura. Uma vez que temos o cosseno, obtemos o seno pela soma trigonométrica e em seguida lembramos que os senos de ângulos suplementares devem ser iguais. Por fim temos tudo que precisamos para calcular a área de cada um dos triângulos individualmente.