Unicentro 2020 matemática

Na figura, Abcd é um quadrado com 2cm de lado, E e G são os pontos médios dos lados DC e Ad, respectivamente, e a circunferência é tangente aos lados AB e BC do quadrado grande.
Se a área do círculo mede xpcm², então o valor do x é
Resposta 6 - 4 . Raiz de 2.
Obrigada!

Boa noite!

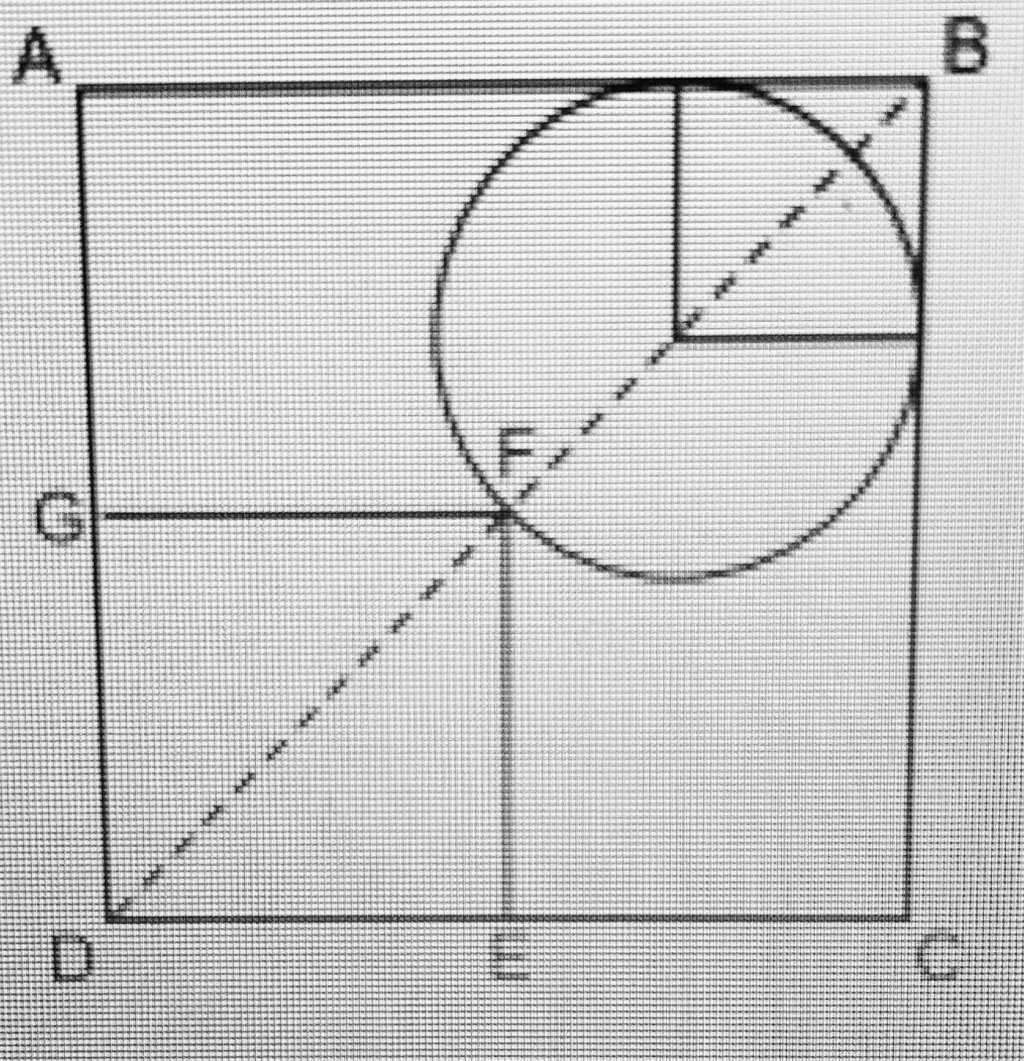
Se o lado do quadrado é 2, sua diagonal mede [latex]2\sqrt{2}[latex], certo?
A distância do ponto DF é a mesma que FB (metade da diagonal), portanto [latex]\sqrt{2}[latex].
Veja, agora, que FB é a medida de um raio, somado com a diagonal de um quadrado de lado 'raio'. Então:
[latex]r+r\sqrt{2}=\sqrt{2}[latex]
[latex]r\left(1+\sqrt{2}\right)=\sqrt{2}[latex]
[latex]r=\frac{\sqrt{2}}{\sqrt{2}+1}[latex]
[latex]r=\frac{\sqrt{2}}{\sqrt{2}+1}\cdot\frac{\sqrt{2}-1}{\sqrt{2}-1}[latex]
[latex]r=\frac{\sqrt{2}\cdot\left(\sqrt{2}-1\right)}{2-1}[latex]
[latex]r=2-\sqrt{2}[latex]

Agora, calculando a área:
[latex]A=\pi\cdot r^2=\pi\cdot\left(2-\sqrt{2}\right)^2[latex]
[latex]A=\pi\cdot\left(4-4\sqrt{2}+2\right)[latex]
[latex]A=\left(6-4\sqrt{2}\right)\pi[latex]

[latex]\boxed{x=6-4\sqrt{2}}[latex]
Espero ter ajudado!