infinito / infinito == 1 ? limite e triangulo retangulo

Bom, eu estava vendo operações aritimeticas com infinitos e fiquei curioso, daí tentei compreender essas ideias usando retas (que são infinitas) e limites, bom, Percebi que em um triangulo retângulo a medida em que α aumenta, a hipotenusa e o cateto oposto também aumentam, e tendem à ter a mesma medida, oque é correto já que seno de 90° é 1, porém o cateto oposto e a hipotenusa tendem ao infinito a medida que α aumenta, então já que o limite do cateto oposto e da hipotenusa a medida que α aumenta é igual à infinito, não seria infinito / infinito nesse caso igual à 1?

Lembrando que o site abaixo dá medidas aproximadas, então onde está escrito α = 90°, é uma aproximação, portanto,dando para formar um triângulo, já que temos um angulo igual à 90° e outro menor que 90°.





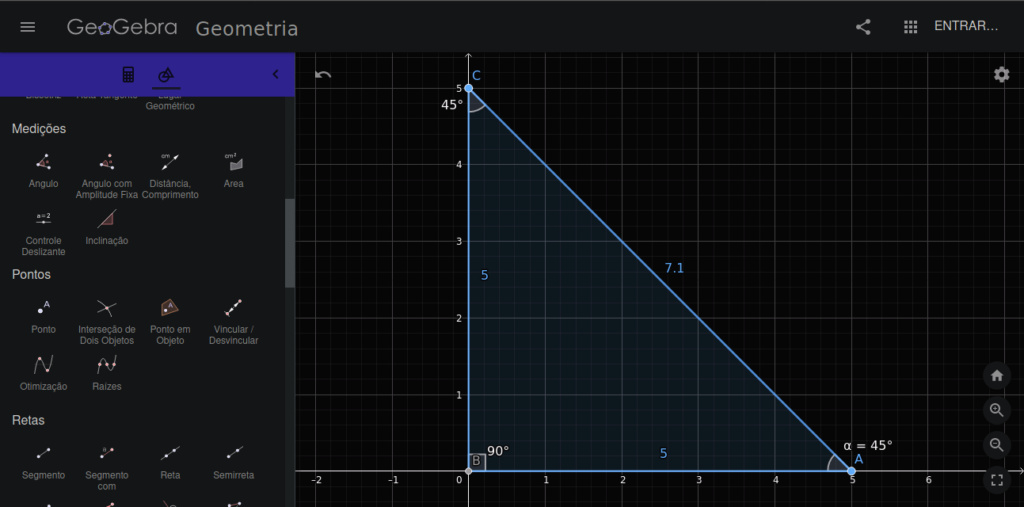
Ao prolongarmos o vertice do triangulo no eixo das ordenadas, percebemos que cateto oposto e hipotenusa tendem à ter medidas iguais, logo, seno de 90 = 1, porém, além disso, cateto oposto e hipotenusa tendem à valores infinitos, podemos "deslizar" o vertice do triangulo no eixo das ordenadas infinitamente sem deixarmos de possuir um triangulo retangulo, e como seno de 90° = 1, nós não deveriamos poder dizer que infinito / infinito == 1 ?

Acontece que a hipotenusa, por ser maior, tende a infinito antes do cateto oposto.

A divisão de infinito por infinito é uma indeterminação.

Muito cuidado ao trabalhar com infinito, que NÃO é um número real.

Eu também pensei assim , mas eu acho que essa ideia da hipotenusa ser maior não se aplica já que não existe um infinito maior que outro, por exemplo os números irracionais periodicos
EX:
3.5555...


Se multiplicarmos esse número por 10, estaremos tirando 1 cinco desse infinito

estaremos tirando 1 elemento de um conjunto infinito, porém ele continua infinito, não faz diferença nenhuma.

x + infinito == infinito

Pensei que se aplicava com hipotenusa e cateto oposto essa ideia, não?

Eu não sabia que nos limites "chegar primeiro" era uma coisa importante nesse caso, já que o que importa é o limite e não a "velocidade" com que se chega nele

Matheus

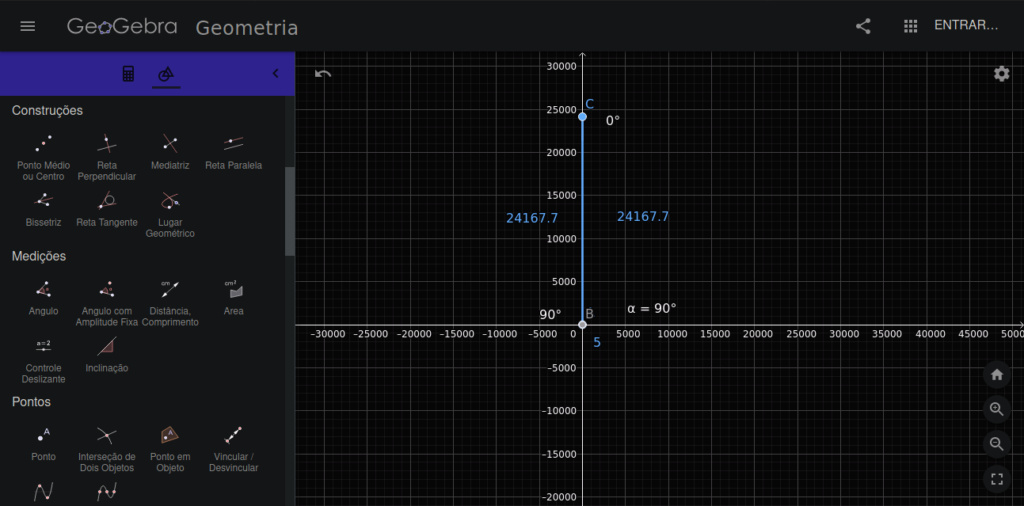
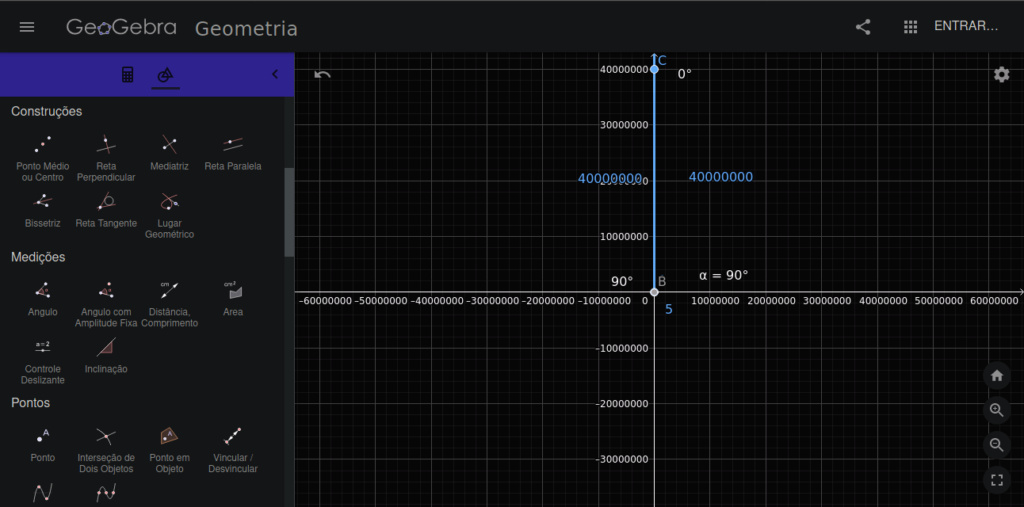
mas quem te disse que as ordenadas dos gráficos 2 e 3 estão no infinito. Uma está em mais ou menos 25 mil e a outra em apenas 40 milhões. Estes são números muito pequenos, nem arranham o pensamento em infinito. Por que? Porque se você consegue escrever (pensar) um número então esse não é o infinito. Dizemos que um n° x está no + infinito quando tomando um n° M, tão grande quanto se queira, temos x > M. Ou seja, M é o máximo que conseguimos imaginar -- mas M não é infinito (e também não é sua borda).

Nesses gráficos não aparece um triângulo, mas uma linha reta, simplesmente porque a linha com que se desenhou é muito mais grossa que a unidade da escala usada; ou seja, apenas por incapacidade de desenhar corretamente. Lembro que, por Euclides, linha não tem largura, apenas lonjura -- desta forma não conseguiríamos ver um linha, somente imaginar ela, e desenhamos para facilitar nosso trabalho.

Ah, e as cotas só aparecem iguais devido a incapacidade do programa de trabalhar com mais precisão.

Ainda, também não me é simpática a ideia mas a verdade é que existem, sim, infinitos maiores do que outros. E isto tem lá sua utilidade em matemática.

Medeiros, eu nunca disse que as coordenadas do gráfico 2 e 3 estão no infinito, nunca, o que eu disse foi que as ordenadas do vertice desse TRIANGULO (sim, TRIANGULO e não uma linha como vc disse, oque acontece é que quando reduzimos a escala de uma figura essa figura ficará tão pequena mais tão pequena que parecerá apenas um ponto ou uma reta, mais se ampliarmos conseguiriamos ver claramente uma figura plana, esse triangulo possui base de 5 unidades e altura de 400 milhões, por isso e somente por isso vc enxerga uma "linha reta" que na verdade deveria ser segundo vc um segmento de reta não? , mas na verdade é um triangulo) poderiam ser extendidas para o infinito, afinal corrija-me se eu estiver errado, o eixo das ordenadas se estende até o infinito para os dois lados não? Eu poderia muito bem com toda certeza aumentar a ordenada do vertice desse triangulo indefinidamente, eu sempre poderia aumentar em 1 unidade a altura desse triangulo retangulo, logo sua altura tende ao infinito à medida em que o angulo tende à 90°


Esse programa mostra 90° porque eu configurei ele para arredondar somente 1 casa decimal, considere onde está escrito α = 90° como sendo :
α =89.99999999999999999999999999999999°, logo, temos um TRIANGULO

Quanto à questão do infinito / infinito == 1, minha duvida continua, afinal como o Elcioschin disse, não importa o quão grande é à altura do triangulo, a hipotenusa sempre será maior, logo, seno de α nunca será igual à 1 OK, mas o seu limite é igual à 1, quanto mais aumentamos sua ordenada, mais proximo de 1 seu seno será. 

É a mesma coisa de progressões geometricas de razão 1 / 2, quando nós calculamos à "soma" desse tipo de progressão nós não estamos calculando a "soma", nós estamos calculando o limite da soma, mas na realidade sabemos que a soma NUNCA será igual à calculada, pois sempre teremos infinitos elementos para somar a essa variavel

Quanto a questão do infinito > que infinito, já entendi já que SIM, existem infinitos maiores

Note que, quando o cateto vertical tende para infinito o cateto horizontal tende para zero.

Assim, no limite, quando tivermos o cateto vertical = ∞, cateto horizontal = 0

Logo não existe mais triângulo

Neste caso a tangente trigonométrica do ângulo entre o cateto horizontal vale tg90º ---> não existe, pois não é real

Veja porque tomar cuidado com infinito:

Quanto vale x = ∞ - ∞ ?

O nosso instinto vai dizer que vale zero. 
Mas o instinto NÃO vale na matemática! É preciso provar:

x = 1/0 - 1/0 ---> x = (1 - 1)/0 ---> x = 0/0 ---> indeterminado

Quando o cateto vertical (oposto) tende ao infinito, o cateto horizontal (adjacente) permanece constante, e a hipotenusa também tende ao infinito.

Oque eu pensei foi o seguinte:
Quanto mais o angulo se aproxima de 90° mais o seno se aproxima de 1
E quanto mais o seno se aproxima de 1, mais o cateto oposto e a hipotenusa se aproximamam de +∞


EX:
cateto oposto      = 3
cateto adjacente = 4
hipotenusa          = 5
sen α                   = 3 / 5 == 0.6


Quanto mais aumentarmos o valor do cateto oposto, mais aumentaremos o valor da hipotenusa e consequentemente mais aumentaremos o valor do angulo e do seno


cateto oposto      = 30
cateto adjacente = 4
hipotenusa          = 30.26...
sen α                   = 30 / 30.26 == 0.9912...

Se aumentarmos o cateto oposto indefinidamente, o seno continuara indefinidamente se aproximando de 1 e o angulo continuara indefinidamente se aproximando de 90°

A medida que cateto oposto se aproxima do +∞, a hipotenusa também se aproxima do +∞, e a razão entre essas medidas se aproxima de 1


EX:
3 / 4 == 0.75

4 / 5 == 0.8

5 / 6 == 0.83....



100000000 / 100000001 == 0.9999....



Minha conclusão é que a medida que dois números reais se aproximam de +∞, a razão entre esses dois números se aproxima de 1


Tenho que estudar mais o CONCEITO de infinito, acho que estou compreendendo ele de forma errada, de qualquer forma vou dar minha duvida nessa thread como resolvida. Obrigado pelas respostas

Neste caso realmente dá 1.
Entenda que cada caso deve ser analisado individualmente e a resposta pode variar de zero a infinito.

matheusG408

No passado o estudo do infinito foi tão complicado que muitos matemáticos importantes dedicaram muito tempo de sua existência para defini-lo.

Hoje o assunto já está sacramentado, e não existem mais dúvidas.

Existem muitos livros dedicados ao assunto.