Força elástica, Atrito estático
2 participantes
PiR2 :: Física :: Mecânica Geral
Página 1 de 1
 Força elástica, Atrito estático
Força elástica, Atrito estático
O sistema a seguir é constituído por dois blocos de massa m1 e m2 que se conectam a uma parede vertical por meio de molas ideais de constantes elásticas k1 e k2, respectivamente. O bloco de massa m2 movimenta-se sem atrito com o solo horizontal, mas entre os blocos existe atrito cujo coeficiente de atrito estático vale "mi".
Inicialmente, os blocos encontra-se em repouso em relação ao solo quando as molas assumem os seus comprimentos naturais. O sistema é deslocado de sua posição de equilíbrio por ação de um agente externo e a seguir abandonado a partir do repouso. Podemos dizer corretamente que a máxima amplitude (delta x max) de deslocamento que mantém os blocos unidos como uma única estrutura, é dada por:
a)
b)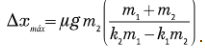
c)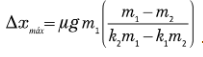
d)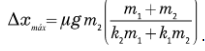
e)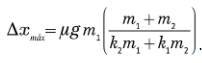
Obrigado desde já.
TomeCostaLima- Iniciante
- Mensagens : 1
Data de inscrição : 04/08/2020
 Re: Força elástica, Atrito estático
Re: Força elástica, Atrito estático
Supondo que esse deslocamento ocorre no sentido positivo ( para direita).
Se o o sistema se mantém unido, a aceleração de todo o sistema, assim como a aceleração de cada bloco devem ser iguais e ter mesmo sentido, além disso, se ambos estão em no comprimento inicial, e ambos blocos não se moveram em relação ao outro durante o processo, a deformação de ambas molas serão iguais:
[latex](k_1+k_2)x=(m_1+m_2)a[/latex]
Agora devemos separar o sistema em dois sistemas. para sabermos o sentido da força de atrito em cada bloco, devemos escolher arbitrariamente qual bloco tenderia a acelerar mais sem a presença do atrito. Suponhamos que o bloco 2 tende a ter maior aceleração, então:
[latex]k_1.x=m_1.a_1\\k_2.x=m_2.a_2\\\dfrac{k_1}{k_2}=\dfrac{m_1}{m_2}.\dfrac{a_1}{a_2}<\dfrac{m_1}{m_2}[/latex]
Essa parte anterior é provavelmente desnecessária, apenas irei utiliza-la para validar minha resposta ao final.
Isso mostra que:
[latex]k_1m_2 < k_2m_1[/latex]
Se o bloco 2, tende a ter uma maior aceleração, o bloco 1 tende a escorregar para direita, logo, no bloco 1, oa trito está para esquerda, e no bloco 2, o atrito está para direita.
equacionando para um dos blocos:
[latex]k_2 x-\mu g m_1=m_2.a\\k_2x-\mu g m_1=m_2\dfrac{(k_1+k_2)x}{m_1+m_2}[/latex]
[latex](m_1k_2+m_2k_2-m_2k_1-m_2k_2)x=\mu g m_1(m_1+m_2)\\x=\mu g m_1\dfrac{m_1+m_2}{k_2m_1-k_1m_2}[/latex]
como ele pede Delta x, o denominador do resultado deve ser positivo. Ai o resultado que encontrei da consideração que a2 tende a acelerar mais que a1 prova que o denominador é positivo. OU seja, se vc fazer a consideração contrário, vc encontraria o sinal do denominador invertido. Se vc considerasse que m1 tende a acelerar mais que m2, o sinal da força de atrito seria invertido, e o denominador estaria "ao contrário" = m2k1-m1k2, mas com a consideração de que a1>a2, esse valor seria positivo. ou seja, ambos resultados estão corretos, dependendo apenas da consideração que o autor fez. Mas então vc deveria adivinhar a consideração do autor ? não, supondo que a suposição feita por vc tivesse sido o contrário da que fiz, vc deveria ter o discernimento de que a suposição contrário daria o resultado encontrado. E como ambos são plausíveis, vc deve ser guiado pelas possíveis opções dadas pelo autor.
Se o o sistema se mantém unido, a aceleração de todo o sistema, assim como a aceleração de cada bloco devem ser iguais e ter mesmo sentido, além disso, se ambos estão em no comprimento inicial, e ambos blocos não se moveram em relação ao outro durante o processo, a deformação de ambas molas serão iguais:
[latex](k_1+k_2)x=(m_1+m_2)a[/latex]
Agora devemos separar o sistema em dois sistemas. para sabermos o sentido da força de atrito em cada bloco, devemos escolher arbitrariamente qual bloco tenderia a acelerar mais sem a presença do atrito. Suponhamos que o bloco 2 tende a ter maior aceleração, então:
[latex]k_1.x=m_1.a_1\\k_2.x=m_2.a_2\\\dfrac{k_1}{k_2}=\dfrac{m_1}{m_2}.\dfrac{a_1}{a_2}<\dfrac{m_1}{m_2}[/latex]
Essa parte anterior é provavelmente desnecessária, apenas irei utiliza-la para validar minha resposta ao final.
Isso mostra que:
[latex]k_1m_2 < k_2m_1[/latex]
Se o bloco 2, tende a ter uma maior aceleração, o bloco 1 tende a escorregar para direita, logo, no bloco 1, oa trito está para esquerda, e no bloco 2, o atrito está para direita.
equacionando para um dos blocos:
[latex]k_2 x-\mu g m_1=m_2.a\\k_2x-\mu g m_1=m_2\dfrac{(k_1+k_2)x}{m_1+m_2}[/latex]
[latex](m_1k_2+m_2k_2-m_2k_1-m_2k_2)x=\mu g m_1(m_1+m_2)\\x=\mu g m_1\dfrac{m_1+m_2}{k_2m_1-k_1m_2}[/latex]
como ele pede Delta x, o denominador do resultado deve ser positivo. Ai o resultado que encontrei da consideração que a2 tende a acelerar mais que a1 prova que o denominador é positivo. OU seja, se vc fazer a consideração contrário, vc encontraria o sinal do denominador invertido. Se vc considerasse que m1 tende a acelerar mais que m2, o sinal da força de atrito seria invertido, e o denominador estaria "ao contrário" = m2k1-m1k2, mas com a consideração de que a1>a2, esse valor seria positivo. ou seja, ambos resultados estão corretos, dependendo apenas da consideração que o autor fez. Mas então vc deveria adivinhar a consideração do autor ? não, supondo que a suposição feita por vc tivesse sido o contrário da que fiz, vc deveria ter o discernimento de que a suposição contrário daria o resultado encontrado. E como ambos são plausíveis, vc deve ser guiado pelas possíveis opções dadas pelo autor.
LPavaNNN- Grupo
Velhos amigos do Fórum
- Mensagens : 933
Data de inscrição : 22/04/2012
Idade : 30
Localização : Goiânia/GO Brasil
TomeCostaLima gosta desta mensagem
 Tópicos semelhantes
Tópicos semelhantes» Por que motivo na iminência de escorregamento a força centrípeta deve ser igual à força de atrito estático?
» Força de atrito estático
» Força de Atrito Estático
» Força de atrito estático
» Força de Atrito Estático
» Força de atrito estático
» Força de Atrito Estático
» Força de atrito estático
» Força de Atrito Estático
PiR2 :: Física :: Mecânica Geral
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












