FME 1 - Questão 108

por jskywalker Seg 13 Jul 2020, 12:51

Se R e S são as relações binárias de A = {x ∈ ℤ | -2 ≤ x ≤ 5} em B = {y ∈ ℤ | -2 ≤ y ≤ 3} definidas por:
x R y ⇔ 2 divide (x-y)
x S y ⇔ (x-1)² = (y-2)²

Pedem-se:
a) as representações cartesianas de R e de S
b) o domínio e a imagem de R e de S
c) R Ո S

por **Emanuel Dias** Seg 13 Jul 2020, 12:58

Olá jskywalker. Peço que digite a questão, assim o mecanismo de busca do google recomenda seu post caso alguém tenha mesma dúvida, é uma das regras do fórum. Assim que fizer isso ajudaremos com a questão. cheers

por jskywalker Seg 13 Jul 2020, 13:27

Foi mal, ainda estou aprendendo a usar o fórum. Já editei. Wink

por **Emanuel Dias** Seg 13 Jul 2020, 14:02

jskywalker escreveu:Foi mal, ainda estou aprendendo a usar o fórum. Já editei.

Sem problemas. Caso possua o gabarito, poste junto também, ajuda quem está tentando resolver.

a)

x R y é uma relação tal que x-y é divisível por 2. Então, x-y é par.

x={-2,-1,0,1,2,3,4,5}
y={-2,-1,0,1,2,3}

x=-2, temos os valores de y possíveis = -2,0,2
x=-1, temos os valores de y possíveis = -1,1,3
x=0 , ............................................ = -2,0,2
Note que, se x é par, os valores de y são os pares, se x é ímpar os valores de y são os ímpares.

Então, os pares ordenados são (x,y)/ x é par ⇒ y é par ou (x,y)/ x é ímpar ⇒ y é ímpar. x e y no intervalo dado, claro.

Para fazer a representação gráfica, basta pegar todos os valores de x e ir variando os y possíveis.

Exemplo: Tomando x=-1, temos y=-1,1,3, então, para x=-1, os pares possíveis são (-1,-1),(-1,1),(-1,3).
Faça para todos os x.

Tente as outras, se não conseguir avise.

por jskywalker Seg 13 Jul 2020, 14:52

Opa, eu já havia tentado, gostaria de saber se esse gráfico é apenas de x R y? Se for o caso, eu acertei. Se não for pedir demais, poderia representar o gráfico de x S y para que eu possa conferir aqui?

Quanto ao gabarito, só tenho da c, que é c) Ø

por **Emanuel Dias** Seg 13 Jul 2020, 15:20

jskywalker escreveu:Opa, eu já havia tentado, gostaria de saber se esse gráfico é apenas de x R y? Se for o caso, eu acertei. Se não for pedir demais, poderia representar o gráfico de x S y para que eu possa conferir aqui?

Quanto ao gabarito, só tenho da c, que é c) Ø

A região em azul escuro são os valores de x e y dado no enunciado, os pontos são resultado da relação x r y

Essa é a representação da relação x R y unicamente.

b)

(x-1)²=(y-2)², x-1=y-2 ou x-1=-(y-2) x-y=-1 ou x+y=-1 com x e y no intervalo dado pelo problema.

Note que, a região pintada de azul é o intervalo do enunciado, as retas são os valores da relação s, restringindo a relação para o intervalo dado, a resposta será a intersecção da região azul escura com as retas.

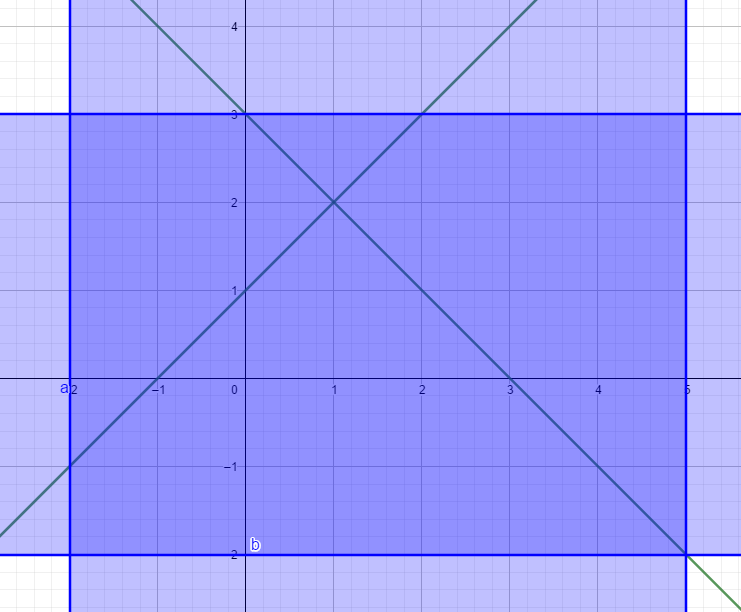
Por fim, essa é a representação simultânea das duas relações, note que não há intersecção (Lembre-se que a relação R são os pontos, e a relação R são as retas, não toda região azul escura).