Geometria Plana e espacial (Área)

por henrickmartins Qui 26 Dez 2019, 23:16

A figura abaixo representa um cubo de aresta 2 cm e um triângulo MNP cujos vértices são os pontos médios de três arestas desse cubo.

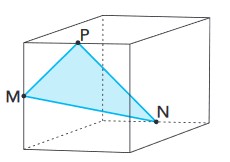
Geometria Plana e espacial (Área) Triang10

A área do triângulo MNP, em cm², mede

Geometria Plana e espacial (Área) Triang11

Resposta: A

Só consegui achar um dos lados usando pitágoras. Tracei linha pra todo lado e não consegui estabelecer nada que fizesse que eu achasse um angulo ou outro lado. Alguém pode dar um help?

Grato.

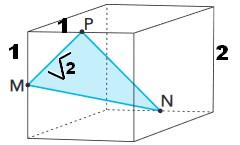
Geometria Plana e espacial (Área) Trizen12

por **Baltuilhe** Sex 27 Dez 2019, 01:13

Boa noite!

Segmento MP vc já encontrou o tamanho.

Para obter o PN:
\overline{PN}^2=2^2+2^2=4+4=8\\\overline{PN}=2\sqrt{2}

Para obter o MN:
\overline{MN}^2=1^2+2^2+1^2=1+4+1=6\\\overline{MN}=\sqrt{6}

Então, temos um triângulo com lados \sqrt{6}, 2\sqrt{2} e um lado \sqrt{2}.

Podemos calcular o ângulo entre os lados PN e MN, então:
\left(\sqrt{2}\right)^2=\left(\sqrt{6}\right)^2+\left(2\sqrt{2}\right)^2-2\cdot\sqrt{6}\cdot 2\sqrt{2}\cdot\cos\theta\\
2=6+8-8\sqrt{3}\cos\theta\\
8\sqrt{3}\cos\theta=6+8-2=12\\
\cos\theta=\dfrac{12}{8\sqrt{3}}=\dfrac{\sqrt{3}}{2}\\
\sin\theta=\sqrt{1-\left(\cos\theta\right)^2}=\sqrt{1-\dfrac{3}{4}}\\
\sin\theta=\sqrt{\dfrac{1}{4}}=\dfrac{1}{2}

A área, portanto:
A=\dfrac{2\sqrt{2}\cdot\sqrt{6}\sin\theta}{2}=\dfrac{2\sqrt{2}\cdot\sqrt{6}\cdot\dfrac{1}{2}}{2}\\
A=\dfrac{\sqrt{12}}{2}=\dfrac{2\sqrt{3}}{2}\\
A=\sqrt{3}

Espero ter ajudado!

por henrickmartins Dom 29 Dez 2019, 01:48

Oi amigo, obrigado por responder minha duvida. Fiquei sem internet por furto dos cabos aqui na região. Coisas do RJ....
Vou postar uma imagem e vou pedir para conferir se suas duas linhas iniciais da resolução foram usandos esses triângulos.

Primeiro o triângulo retângulo PRN. Achando MN.
Em seguida juntou os dois triângulos MAD + MDN.
Foi isso, ou outra coisa?

Abraços

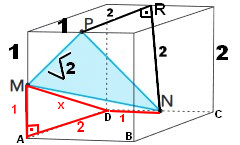
Geometria Plana e espacial (Área) Triang12

por **Baltuilhe** Dom 29 Dez 2019, 03:08

henrickmartins escreveu:Oi amigo, obrigado por responder minha duvida. Fiquei sem internet por furto dos cabos aqui na região. Coisas do RJ....
Vou postar uma imagem e vou pedir para conferir se suas duas linhas iniciais da resolução foram usandos esses triângulos.

Primeiro o triângulo retângulo PRN. Achando MN.
Em seguida juntou os dois triângulos MAD + MDN.
Foi isso, ou outra coisa?

Abraços

Boa noite!

Foi isso mesmo! Smile

por henrickmartins Dom 29 Dez 2019, 12:22

Muito bom, amigo!
Obrigado

por henrickmartins Dom 29 Dez 2019, 18:07

Ah. Para Área usei Herão.
No início parece que vai ser o demônio, mas aparecem duas diferenças de dois quadrados, simplificando muita coisa e no fim também dá raiz de 3.
Abraço.