medida do segmento e área da circunferência

por marcelofarias501 Qua 24 Jul 2019, 14:41

O síndico de um condomínio resolveu construir um jardim na entrada do prédio (aqui tem a imagem de um quadrado junto com uma semicircunferência)

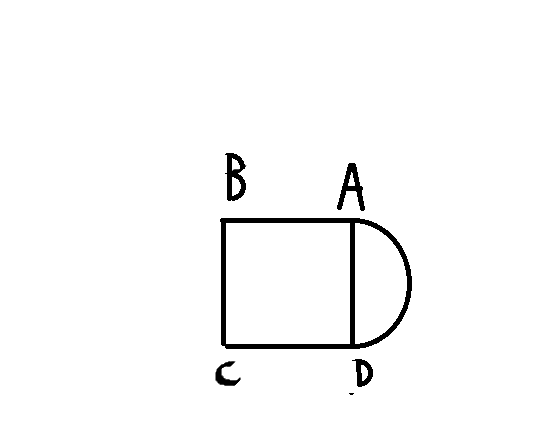
medida do segmento e área da circunferência Questz10

Sabe-se que as medidas dos segmentos AB, BC, CD e AD são iguais. O contorno do jardim que liga A a D é uma semicircunferência. Tomando o valor de pi como 3,1 e a área do jardim igual a 22,2 metros quadrados, é correto afirmar que a medida de AB é:

a) 5m
b) 3,5m
c) 4,5m
d) 3m
e) 4m

por **Leonardo Mariano** Qua 24 Jul 2019, 15:07

Área do quadrado = A1;
Área da semicircunferência = A2;
AB = x
A_1=x.x \\
A_2 = \frac{\pi .(\frac{x}{2})^2}{2} \\
A_1 + A_2 = 22,2 \rightarrow x.x + \frac{\pi .(\frac{x}{2})^2}{2} = 22,2 \rightarrow x^2 + \pi .\frac{x^2}{8} = 22,2 \rightarrow \frac{(8 + 3,1)x^2}{8} = 22,2 \rightarrow x^2 =\frac{22,2.8}{11,1} \rightarrow x = \sqrt{\frac{177,6}{11,1}} \rightarrow x = \sqrt{16}\rightarrow x=4 \: m

por marcelofarias501 Qua 24 Jul 2019, 16:24

você começou com x.x + pi.(x/2)^2/2 = 22,2 e depois conseguiu x^2+pi.x^2/8=22,2

não entendi

Da onde veio esse x^2/8?

Ah, acho que entendi. Você pegou o x^2/4/2/1 e então multiplicou x^2/4 por 1/2

Agora, da onde veio esse 22,2=(8+3,1).x^2/8 ?

O x^2 você manteve, o 3,1 do pi também. Porém, esse + entre o 8 e o 3,1 é o mesmo que tinha entre o x^2 e o pi há uma etapa atrás, portanto isso quer dizer que você igualou x^2 a 8? Porque eu não consigo entender como x^2 = 8

por **Elcioschin** Qua 24 Jul 2019, 17:05

x² + pi.x²/8 = 22,2

(8.x² + pi.x²)/8 = 22,2

x².(8 + pi) = 22,2.8

x².(8 + 3,1) = 177,6

x².11,1 = 177,6

x² = 16

x = 4

por marcelofarias501 Qua 24 Jul 2019, 17:49

Você multiplicou todos por 8 em x² + pi.x²)/8? Ou foi só o x^2 que já somava com pi que vc multiplicou por 8? E por que multiplicar justamente por 8? Digo aqui:

(8.x² + pi.x²)/8

E o que aconteceu com os dois x ao quadrado que tinham dentro do parêntese para ficar só x^2 do lado de fora?

Quero dizer, ficou desse jeito depois: x².(8 + pi)

por **Elcioschin** Qua 24 Jul 2019, 18:13

Da 1ª para a 2ª linha eu apenas somei as frações

x² + pi.x²/8 = 8.x²/8 + pi.x²/8 = 8.(x²/8) + pi.(x²/8)

Basta agora colocar (x²/8) em evidência: (x²/8).(8 + pi) = x².(8 + pi)/8

Suas dúvidas sobre a questão resumem-se a contas simples do Ensino Fundamental.
Acontece que você já está no Ensino Médio. Isto significa que você precisa reestudar as bases do Ensino Fundamental.