Equação cúbica irracional - Iezzi

Olá, pessoal! 

Estou tentando resolver a questão 383 do volume 1 da coleção Fundamentos da Matemática Elementar do Iezzi, que consiste na seguinte equação: 



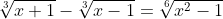
Estou tentando resolver utilizando a identidade do cubo da diferença, manifesta por:



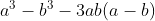
Contudo, não consegui resolver e estou caindo em pedaços cada vez mais complexos, como por exemplo, potências elevadas à sexta! 

O resultado é:



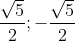
Poderiam me ajudar?

Grato!

Lembre-se que (a - b)³ = a³ - 3.a².b + 3.a.b² - b³ = a³ - b³ - 3.a.b.(a - b)

Neste caso temos a = ∛(x + 1), b = ∛(x - 1)

Basta elevar a equação original ao cubo e simplificar. O gabarito está correto

Mostre o seu passo-a-passo para comentarmos (e não vai ficando mais complexo não!)

Elcioschin escreveu:Lembre-se que (a - b)³ = a³ - 3.a².b + 3.a.b² - b³ = a³ - b³ - 3.a.b.(a - b)

Neste caso temos a = ∛(x + 1), b = ∛(x - 1)

Basta elevar a equação original ao cubo e simplificar. O gabarito está correto

Mostre o seu passo-a-passo para comentarmos (e não vai ficando mais complexo não!)

Obrigado pela dica, Elcio!

Fiz o seguinte, usando a identidade:



Em seguida, tentei usar uma técnica para colocar todos os radicais sob o mesmo índice:



E é aqui que começam os problemas, que penso que cometi um erro, onde decompus  
 




Passando para o outro lado e alterando os sinais, temos:



É a partir daqui que não consigo desenvolver mais, sempre chegando a coisas mais complexas, até mesmo equações de sexto grau.

Peço que me aponte o erro que cometi pois não sei se pensei corretamente.

Grato.

∛(x + 1) -  ∛(x - 1) = ⁶√(x² - 1) ---> Elevando ao cubo:

[∛(x + 1) -  ∛(x - 1)]³ = [⁶√(x² - 1)]³

(x + 1) - 3.∛[(x + 1)²].∛(x - 1) + 3.∛(x + 1).∛[(x - 1)²] - (x - 1) =  [⁶√(x² - 1)]³

2 - 3.∛[(x + 1).(x - 1)].∛(x + 1) + 3.∛[(x + 1).(x - 1)].∛(x - 1) = [⁶√(x² - 1)]³

2 - 3.∛(x² 1).∛(x + 1) + 3.∛(x² - 1).∛(x - 1) = [⁶√(x² - 1)]³

2 - 3.∛(x² - 1).{∛(x + 1) - ∛(x - 1)} = [⁶√(x² - 1)]³ ---> Trecho em vermelho é o original

2 - 3.∛(x² - 1).⁶√(x² - 1) = [⁶√(x² - 1)]³

2 - 3.(x² - 1)^1/3.(x² - 1)^1/6 = (x² - 1)^1/2

2 - 3.(x² - 1)^1/2 = (x² - 1)^1/2

4.(x² - 1)^1/2 = 2 ---> (x² - 1)^1/2 = 1/2 ---> Elevando ao quadrado:

x² - 1 = 1/4 ---> x² = 5/4 ---> x = ± √5/2

Consegui entender a dinâmica do cálculo, mas no entanto, restou-me uma dúvida.

Elcio, poderia me explicar como após o termo:

(x + 1) - 3.∛[(x + 1)²].∛(x - 1) + 3.∛(x + 1).∛[(x - 1)²] - (x - 1) =  [⁶√(x² - 1)]³


Acabou sumindo e dando origem a:

2 - 3.∛[(x + 1).(x - 1)].∛(x + 1) + 3.∛[(x + 1).(x - 1)].∛(x - 1) = [⁶√(x² - 1)]³

Eu não consegui entender como esse x elevado ao quadrado sumiu e você não o transformou em um quadrado perfeito, Elcio.

Foi feita uma fatoração?
Grato.

Tanto no 2º como no 3º termo existem termos iguais, que podem ser colocados em evidência:

- 3.∛[(x + 1)²].∛(x - 1) + 3.∛(x + 1).∛[(x - 1)²]

- 3.∛(x + 1).∛(x + 1).∛(x - 1) + 3.∛(x + 1)∛(x - 1).∛(x - 1)

- 3.∛(x + 1).∛(x² - 1) + 3.∛(x² - 1).∛(x - 1)

- 3.∛(x² - 1).[∛(x + 1) - ∛(x - 1)]

Elcio, obrigado pela luz que me deu, estou quase entendendo, mas só falta uma coisa hehe

É o seguinte, no termo fatorado a seguir:

- 3.∛(x² - 1).[∛(x + 1) - ∛(x - 1)]

Pude compreender a separação dos quadrados para fazer surgir termos comuns, o que está OK. 

Porém, no termo a seguir, não compreendi como você operou para que o termo que postei acima, pudesse se transformar em:

2 - 3.∛(x² - 1).⁶√(x² - 1) = [⁶√(x² - 1)]³


Gostaria de entender o que foi feito com o termo (x+1) que estava dentro da parte fatorada, podendo assim concluir a questão e refazê-la.

Grato.

Eu expliquei isto na minha solução original:

2 - 3.∛(x² - 1).{∛(x + 1) - ∛(x - 1)} = ⁶√(x² - 1)]³ ---> Trecho em vermelho é o original

Eis o o enunciado original da sua questão: ∛(x + 1) -  ∛(x - 1) = ⁶√(x² - 1)

Basta substituir o vermelho da linha 2 pelo 2º membro da linha 3

outra solução:


Inicialmente, iremos utilizar as seguintes identidades durante o problema:

(a - b)^2 = a^2 - 2ab + b^2

a^3 - b^3 = (a-b)(a^2 + ab + b^2)


Vamos, agora, atacar o problema.

Tome

a = \sqrt[3]{x+1}

b = \sqrt[3]{x-1}

Assim,

\left\{\begin{matrix}
a - b   = \sqrt{ab} \\ 
a^3 - b^3 = 2 
\end{matrix}\right.

Utilizando a identidade mostrada, chegamos em:

(a-b)(a^2 + ab + b^2) = 2

E elevando a primeira equação ao quadrado, tem-se:

a^2 -2ab + b^2 = ab

Logo,


(\sqrt{ab})(4ab) = 2 \ \rightarrow  \ (ab)^3 = \frac{1}{4}


Usando que  a = \sqrt[3]{x+1}   e que  b = \sqrt[3]{x-1}

Chegamos em  x^2 - 1 = \frac{1}{4} \ \rightarrow  \ x = \pm \frac{\sqrt5}{2}

Outra forma:

\\\sqrt[3]{x+1}-\sqrt[3]{x-1}=\sqrt[6]{x^2-1}\\\\\frac{\sqrt[3]{x+1}}{\sqrt[3]{x-1}}-1=\frac{\sqrt[6]{x^2-1}}{\sqrt[3]{x-1}}\,\,\,\,\,\,\,(I)\\\\\\Se\,\,\,\sqrt[3]{x-1}>0\\\\(I):\sqrt[3]{\frac{x+1}{x-1}}-1=\sqrt[6]{\frac{{x+1}}{{x-1}}}

\\Se\,\,\,\sqrt[3]{x-1}<0\\\\(I):\sqrt[3]{\frac{x+1}{x-1}}-1=-\sqrt[6]{\frac{{x+1}}{{x-1}}}

Agora você tem duas equações "a² - a - 1 = 0" e "a² + a - 1 = 0", resolvendo elas você irá encontrar o resultado.