Cálculo da área

Bom dia, Caio!

Bom, essa é uma questão de analítica. Vamos primeiro desenrolar a equação da curva: elevando ambos os termos ao quadrado, temos:

y²=4x - x²

Igualando a 0:
x² -4x + y²=0

Agora, veja que a equação se assemelha à de uma circunferência, que é do tipo (x-a)² + (y-b)²=R², então vamos ter que completar quadrados:

(x-2)² -4 + (y-0)²=0
(x-2)² + (y-0)²=4
(x-2)² + (y-0)²=2²

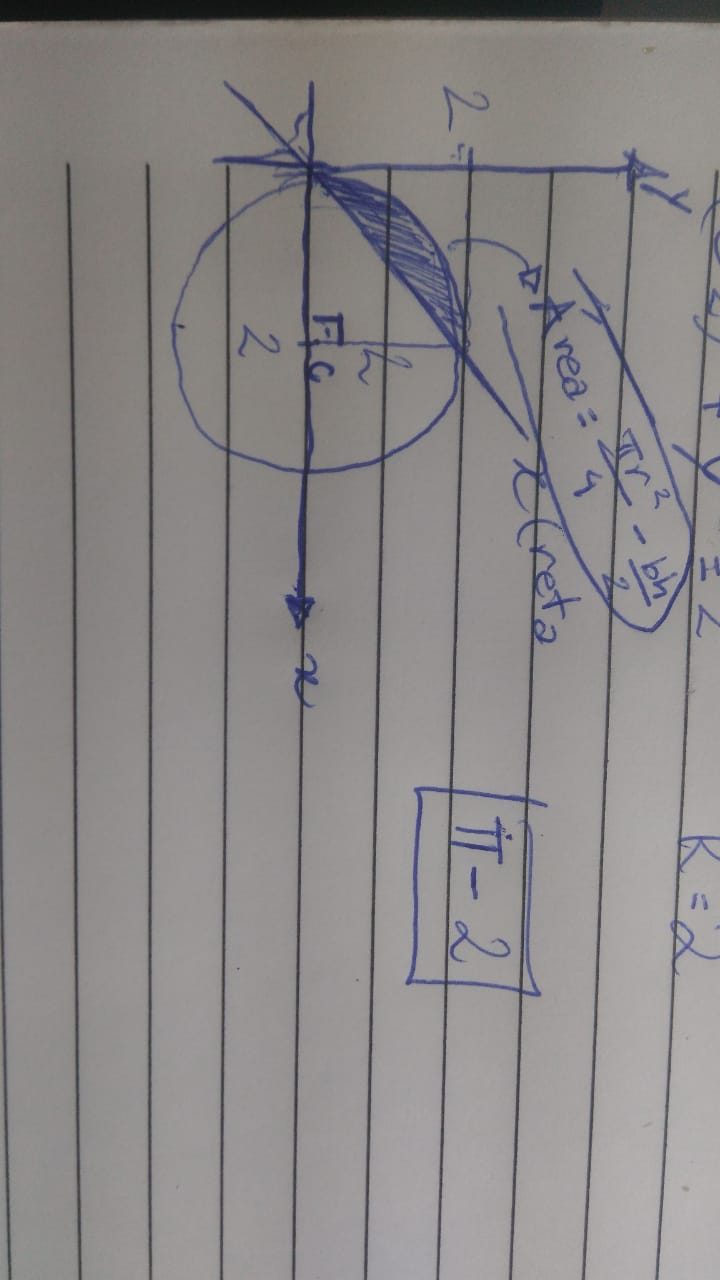
Bom, agora temos uma circunferência de centro C(2, 0) e de raio 2; a reta em questão é uma identidade, ela corta os quadrantes 1 e 3, fazendo a bissetriz e dividindo o ângulo de 90° ao meio, os pontos dela sempre serão (1, 1), (2, 2), ..., (n, n). Sabendo disso e tendo em vista que a nossa circunferência  tem raio 2 e centro 2, a borda extrema superior da mesma é no ponto (2, 2), veja que é um ponto de interseção da extremidade da circunferência e da reta . O outro ponto em que elas se tocam é no (0, 0), pois a reta passa por ele (x=y) e a circunferência também. Na figura que for montada, a reta vai  ser a hipotenusa de um triângulo de lado 2 e altura 2 (que vão ser os raios da circunferência). A área de 1/4 da circunferência é (pi*r²)/4 = 4pi/4= pi; a área que a reta corta é exatamente 1/4 da circunferência menos a área do triângulo.

pi - 2, alternativa B.

Segue imagem para melhor compreensão.

excelente resolução,obrigado!