(ESPM) Analise combinatória

Relembrando a primeira mensagem :

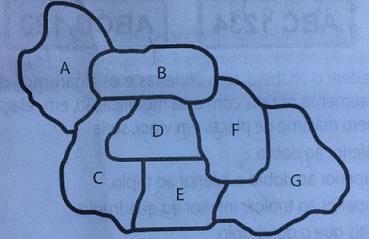
Os 7 países do mapa abaixo devem ser coloridos com 4 cores distintas, de modo que os fronteiriços devem ter cores diferentes, e os países A e D, a mesma cor. O número de maneiras distintas de se efetuar esse trabalho é igual a:


a)48
b)72
c)80
d)96
e)120


Alguém consegue me ajudar ?

sim se começar de E tem 4 possibilidades
mas se for de A,B ou C  e depois o que sobrou nao implica que E=1 pois E#B?
exemplo
(verde,azul,lilas,rosa)
A= verde
B=azul
c=lilas
d=verde

e agora como eu sei que E#B restriçao  E#B#C#D
logo E=rosa pois a unica que restou pois ela nao pode ser nem c ou d pois esta em fronteira e nem igual b pela restriçao e como c,d,b estao em fronteira tem que ser diferentes entre si?

mas acho que quiz dizer se for A,c depois no E  ai vai ter 2 possibilidades mas do mesmo modo E#B logo B=1

Se E # B, a única obrigação inicial é D = A

Nós estamos partindo de A e terminando em G

A ---> 4 possibilidades
B ---> 3 possibilidades (excluída apenas a cor de A)
C ---> 2 possibilidades (excluídas a cor de A e de B)
D ---> 1 possibilidade (tem que ser igual a cor de A)
E ---> 2 possibilidades (excluídas a cor de C e de D)
F ---> 1 possibilidade (excluídas a cor de B, D e E)
G ---> 2 possibilidades (excluídas a cor de E e F)

E ---> 2 possibilidades (excluídas a cor de C e de D) voce nao esta levando em conta que (B) nao pode ser igual a (E) pela propria restriçao inicial.

Perfeito, agora entendi:

E # B ---> Pela hipótese inicial
E # C e E # D ---> devido fazer fronteira com C e D
Logo, E = 1

A = 4
B = 3
C = 2
D = 1
E = 1
F = 1
G = 2 ---> Total parcial = 48

Para E = B

A = 4
B = 3
C = 2
D = 1
E = 1
F = 2
G = 2 ---> Total = 96

Total geral = 48 + 96 = 144 ---> Continua não coincidindo com o gabarito.

Para E = B

A = 4
B = 3
C = 2
D = 1
E = 1
F = 1
G = 2 ---> Total = 48

agora so esqueceu que E=B e (F) so esta em fronteira com E,B,D
como E=B e D #B resta duas cores para F

Correto

Neste caso, para E = B --> 96 possibilidades

Total Geral = 498 + 96 = 144

É possível encontrar o valor que consta no gabarito (120), mas o enunciado está muito mal redigido. Existem dois problemas com ele:

Primeiro: é impossível usar uma cor diferente para cada vizinho porque só existem 4 cores disponíveis e 3 dos países (D, E e F) fazem fronteira com 4 outros. Assim, deve se considerar que E e/ou F podem ser da mesma cor de D.

Segundo: o examinador esqueceu de mencionar que ele queria o número de combinações utilizando o menor número possível de cores repetidas entre vizinhos. Voltando ao primeiro ponto, é inevitável que E ou F repitam a cor de D, mas é possível que F seja diferente de todos os seus vizinhos quando D e E são da mesma cor.

Com isso em mente, é possível começar a resolver o exercício.

A análise começa de forma simples: o País A pode ter qualquer uma das 4 cores; o País B pode ter qualquer uma das 3 restantes; o País C pode ter qualquer uma entre as 2 restantes; e o País D só pode ter a cor do País A. Até agora temos:

4*3*2*1

O caso do País E se divide em 2: E pode ter a mesma cor de B; ou E pode ter uma cor diferente de B.

No primeiro caso, a única possibilidade de cor para E é a mesma de B, enquanto que para F temos 2 possibilidades (lembrando que este deve ser diferente tanto de E (e B) quanto de D). O País G sempre poderá ser pintado de uma das duas cores não utilizadas por seus vizinhos. Dessa forma, temos:

4*3*2*1*1*2*2 = 96

No segundo caso, E tem cor diferente tanto de B (conforme estabelecemos) como de C, que é seu vizinho. Assim, o País E pode ter qualquer uma das duas cores restantes. Agora os 3 vizinhos a oeste de F possuirão cores diferentes. Logo, só existe uma possibilidade de cor para F. G continua tendo duas possibilidades. Em termos matemáticos, temos:

4*3*2*1*2*1*1 = 96

Se somarmos os valores obtidos em ambos os cenários, iremos obter o número total de combinações: 96+96 = 192

Agora precisamos calcular quantas dessas 192 combinações só utilizam 3 cores, já que o enunciado especifica que só quer combinações de 4 cores.

Utilizamos aqui o mesmo raciocínio empregado acima, mas removendo uma cor do nosso repertório. Primeiro removemos qualquer uma das 4 cores e teremos (de A até D):

3*2*1*1

Para o caso de B = E:

3*2*1*1*2*1*1 = 12

Lembrando que G só pode ter uma cor já que seus vizinhos tomaram as outras 2 disponíveis.

E para B diferente de E:

3*2*1*1*2*1*1 = 6

Novamente somamos os dois casos: 12+6 = 18

Por fim, falta permutar essas 18 combinações pelas cores que podemos remover. Por exemplo, se no caso acima removemos a cor H, ainda é possível repetir o procedimento removendo I,J e K. Então, o número total de combinações que utilizam apenas 3 cores é:

4*18 = 72

E finalmente conseguimos chegar ao nosso resultado subtraindo 72 do número total de combinações possíveis:

192 - 72 = 120

Espero que tenha sido claro o suficiente. Esse é um exercício bem chato de resolver.