Triângulos e áreas

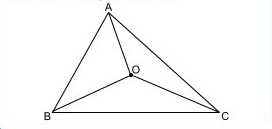
O triângulo ABC da figura é retângulo em A e os triângulos OAB, OAC e OBC são equivalentes (mesma área). Sendo BC = 18 cm, determine OA.



R: 6 cm.

Pessoal, essa eu não tenho palpite de como se resolve. Supus que, como as áreas são equivalentes e chamando de "x" essas áreas, teríamos Sabc = Saob + Soac + Sobc --> b.h/2 = x + x + x --> 18h/2 = 3x --> 9h = 3x --> x = 3h, mas não sei se isso auxilia na resolução.
Alguém poderia ajudar na questão ? Obrigado.

ERRATA

AO/OM = 2/1  ---------> AO = (2/3).AM -----> AO = 6 cm


OBS:

Baricentro é o centro de massa, ou centro geográfico, ou centro de equilíbrio, da figura. Para um triângulo, ele ocorre no encontro das medianas.

Mediana é o segmento que vai do vértice ao ponto médio do lado oposto. Devido a isto, uma mediana divide um triângulo em dois de áreas iguais.

Propriedade: o baricentro divide a mediana na razão 2 : 1 em relação ao vértice.

Perfeito, Mestre Medeiros!!!
Muito obrigado, explicação perfeita!

Ps: o senhor está sumido daqui do fórum. Não abandone nós, pobres (e desprovidos de inteligência "exata") vestibulandos. hahaha

Ah, Medeiros, só uma pergunta: pelo fato de  ser um âng reto eu automaticamente posso considerar M, além de ponto médio, como também circuncentro ? A gente enxerga isso pois será o ponto de encontro das mediatrizes, é isso ?

Bom retorno ao colega Medeiros, sempre com excelentes resoluções!!!

Propriedade: Todo triângulo retângulo é inscritível numa semicircunferência. Neste caso M é o centro da circunferência circunscrita ao triângulo,.
Nesta questão ---> raio R = MA = MB = MC = 9

Perfeito, Mestre Elcio! Muito obrigado pelas ajudas, aos dois.

Percebo que eu devia ter deixado mais claro o raciocínio usado. Pensei assim:

Se os triângulos OAB, OAC e OBC têm áreas iguais então os segmentos OA, OB e OC são pedaços das medianas ⁽¹⁾ e O é o baricentro⁽²⁾. Portanto, prolongando-se AO até encontrar o lado oposto em M, temos que AM é uma mediana onde M é o ponto médio do lado BC.

Se  é ângulo reto, BC é hipotenusa e o triângulo ABC está inscrito numa semicircunferência, com BC obviamente sendo o diâmetro. Assim, M é o circuncentro e MB, MC e MA são raios. Então sabemos a medida do raio AM.

Como AM também é mediana e O é baricentro, e sabemos que este divide a mediana na razão 2:1 a partir do vértice, obtemos a medida de AO =(2/3)*AM.

⁽¹⁾ segmento que liga o vértice ao ponto médio do lado oposto. As três medianas de um triângulo o dividem em seis triângulos de áreas iguais.

⁽²⁾ encontro das medianas.

_______________________________
JohnnyC, sou velho mas não sou mestre (o Élcio é -- mestre, claro), sou mais um entusiasta como vocês e colega de vocês. Um abraço.

Grato pelas boas vindas, Élcio. Um abraço.