Equação do 2º grau/raízes
+3
gelleis
Adam Zunoeta
abelardo
7 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 2
Página 1 de 2 • 1, 2 
 Equação do 2º grau/raízes
Equação do 2º grau/raízes
(Questão retirada do livro de Gelson Iezzi) Determine m na equação do 2º grau x^2 +2mx +3m=0) para que tenha uma única raiz entre
para que tenha uma única raiz entre 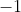 e
e  .
.
R/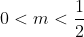
Existem três possibilidades:
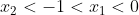 ou
ou
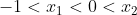 ou
ou
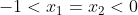
e a partir de uma dessas condições poderia criar relações com a discriminante, com a multiplicação do coeficiente a com as respectivas imagens de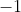 e
e  ; com a soma da raízes ... Como resolver essa resenha?
; com a soma da raízes ... Como resolver essa resenha?
R/
Existem três possibilidades:
e a partir de uma dessas condições poderia criar relações com a discriminante, com a multiplicação do coeficiente a com as respectivas imagens de

abelardo- Grupo
Velhos amigos do Fórum
- Mensagens : 777
Data de inscrição : 12/03/2011
Idade : 32
Localização : Sertânia, Pernambuco, Brasil
 Re: Equação do 2º grau/raízes
Re: Equação do 2º grau/raízes

Última edição por Adam Zunoeta em Qui 23 Jun 2011, 23:20, editado 1 vez(es) (Motivo da edição : Corrigir Português)

Adam Zunoeta- Monitor

- Mensagens : 4223
Data de inscrição : 25/08/2010
Idade : 35
Localização : Cuiabá
 Re: Equação do 2º grau/raízes
Re: Equação do 2º grau/raízes
Não entendi o por que de f(0)*f(-1)=0.. para que essa multiplicação resulte em zero, um dos fatores tem que ser zero, mas nesse caso indica que f(0) ou f(-1) é raiz da equação dada.. onde é que estou viajando?

abelardo- Grupo
Velhos amigos do Fórum
- Mensagens : 777
Data de inscrição : 12/03/2011
Idade : 32
Localização : Sertânia, Pernambuco, Brasil
 Re: Equação do 2º grau/raízes
Re: Equação do 2º grau/raízes
Da Extensão do Teorema de Bolzano vem,
Se f(a)*f(b)=0, "a" ou "b" (ou ambos) é raiz de f.

Se f(a)*f(b)=0, "a" ou "b" (ou ambos) é raiz de f.


Adam Zunoeta- Monitor

- Mensagens : 4223
Data de inscrição : 25/08/2010
Idade : 35
Localização : Cuiabá
 Re: Equação do 2º grau/raízes
Re: Equação do 2º grau/raízes
Pow cara, nunca conseguiria responder isso assim. Eu cheguei a resposta, mas tive que olhar o gabarito primeiro e depois de testar as três possibilidades, eu vi que só uma atendia a questão...

abelardo- Grupo
Velhos amigos do Fórum
- Mensagens : 777
Data de inscrição : 12/03/2011
Idade : 32
Localização : Sertânia, Pernambuco, Brasil
 Re: Equação do 2º grau/raízes
Re: Equação do 2º grau/raízes
Encontrei uma apostila no site rumoaoita falando sobre o Teorema de Bolzano... mas acho melhor estudar a fundo mesmo quando estiver revisando polinômios. Haveria outra forma de responder só tendo o conhecimento sobre função do segundo grau?(estou estudando pela coleção do Iezzi, é o volume 1)..

abelardo- Grupo
Velhos amigos do Fórum
- Mensagens : 777
Data de inscrição : 12/03/2011
Idade : 32
Localização : Sertânia, Pernambuco, Brasil
 Re: Equação do 2º grau/raízes
Re: Equação do 2º grau/raízes
Haveria outra forma de responder só tendo o conhecimento sobre função do segundo grau?(estou estudando pela coleção do Iezzi, é o volume 1).
Provavelmente mais eu não conheço, você sabe a página e o número desse exercício ?
Provavelmente mais eu não conheço, você sabe a página e o número desse exercício ?

Adam Zunoeta- Monitor

- Mensagens : 4223
Data de inscrição : 25/08/2010
Idade : 35
Localização : Cuiabá
 Re: Equação do 2º grau/raízes
Re: Equação do 2º grau/raízes
Pág 179, questão 342. A questão 343 é bem parecida. Obrigado mesmo pela atenção.

abelardo- Grupo
Velhos amigos do Fórum
- Mensagens : 777
Data de inscrição : 12/03/2011
Idade : 32
Localização : Sertânia, Pernambuco, Brasil
 Re: Equação do 2º grau/raízes
Re: Equação do 2º grau/raízes
(3m-2)x²+2mx+3m=0
Pensei assim......
Como a raiz deve estar entre -1 e 0 temos:
Para x=-1
3m-2-2m+3m=0
m=1/2
Para x=0
m=0
Esses são os valores extremos que m pode assumir uma vez que as possíveis raízes que f(x)=(3m-2)x²+2mx+3m assumem dependem estritamente do intervalo ]-1,0[
Então todos os demais valores de "m" devem estar contidos no intervalo entre os extremos de "m"
Portanto:
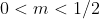
Pensei assim......
Como a raiz deve estar entre -1 e 0 temos:
Para x=-1
3m-2-2m+3m=0
m=1/2
Para x=0
m=0
Esses são os valores extremos que m pode assumir uma vez que as possíveis raízes que f(x)=(3m-2)x²+2mx+3m assumem dependem estritamente do intervalo ]-1,0[
Então todos os demais valores de "m" devem estar contidos no intervalo entre os extremos de "m"
Portanto:

Adam Zunoeta- Monitor

- Mensagens : 4223
Data de inscrição : 25/08/2010
Idade : 35
Localização : Cuiabá
 Re: Equação do 2º grau/raízes
Re: Equação do 2º grau/raízes
Agora ficou mais claro. O teorema de Bolzano é elegante, mas dessa última forma como você fez ficou bem melhor de entender. Essa coisa de translação do gráfico é parecido com geometria analítica.. brigadão.;

abelardo- Grupo
Velhos amigos do Fórum
- Mensagens : 777
Data de inscrição : 12/03/2011
Idade : 32
Localização : Sertânia, Pernambuco, Brasil
Página 1 de 2 • 1, 2 
 Tópicos semelhantes
Tópicos semelhantes» Raízes de equação de grau 3
» raízes equação 3º grau
» Raízes - 2º grau (equação)
» Raízes de equação de grau 4
» Raizes equação do 2 e 3 grau.
» raízes equação 3º grau
» Raízes - 2º grau (equação)
» Raízes de equação de grau 4
» Raizes equação do 2 e 3 grau.
PiR2 :: Matemática :: Álgebra
Página 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos












