Função Periódica

por Victor Luz Dom 18 Fev 2018, 21:38

Sendo f: R -> R uma função periódica de período p>0, classifique as afirmações a seguir em V (verdadeira) ou F (falsa).

( ) A função g(x)= f(2x) é periódica de período 2p.
( ) A função h(x)=f(x/2) é periódica de período p/2
( ) A função f(x)= (x+q), onde q é uma constante positiva, não é periódica.

gabarito:

por **Euclides** Dom 18 Fev 2018, 21:58

Tome como exemplo: y=sen(x), periodo 2pi

- sen(2x), periodo pi
- sen(x/2), periodo 4pi

em sen(x+q) a constante positiva somada apenas translada a função para a esquerda, sem alterar o período.

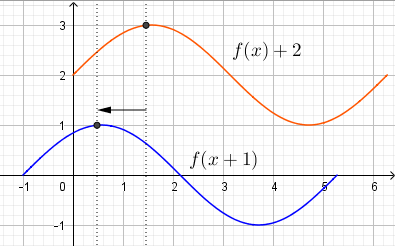
Função Periódica Fig.N

por Victor Luz Dom 18 Fev 2018, 22:05

Euclides escreveu:Tome como exemplo: y=sen(x), periodo 2pi

- sen(2x), periodo pi
- sen(x/2), periodo 4pi

em sen(x+q) a constante positiva somada apenas translada a função para a esquerda, sem alterar o período.

Obrigado Mestre Euclides, mas no caso, a função f(2x) teria período 2p?
Esse enunciado me deixou confuso pois ele não diz qual a lei da função.
Aliás eu encontrei o gabarito, acabei de editar o tópico, perdão por postar sem o gabarito.

por **Euclides** Dom 18 Fev 2018, 22:11

Ele fala genericamente de funções periódicas. Tomei como exemplo a função f(x)=sen(x)

sen(x) tem período 2pi
sen(2x) tem período pi

sen(x+pi/6) tem o mesmo período de sen(x). FFF

por Victor Luz Seg 19 Fev 2018, 08:20

Valeu Mestre, muito obrigado.
Com a função seno ficou muito mais claro de ver as mudanças no período.

por Victor4610 Sex 04 maio 2018, 18:00

Euclides escreveu:Tome como exemplo: y=sen(x), periodo 2pi

- sen(2x), periodo pi
- sen(x/2), periodo 4pi

em sen(x+q) a constante positiva somada apenas translada a função para a esquerda, sem alterar o período.

Não estou conseguindo entender como achou os períodos das funções genéricas do enunciado... alguém poderia me ajudar ? Já tentei procurar a informação de como fazer isso em algumas videoaulas, mas não encontrei nada.

por **Elcioschin** Sex 04 maio 2018, 18:21

Qualquer função trigonométrica (que é periódica) f(x) tem período 2.pi (é o caso da 1ª volta no círculo trigonométrica, por exemplo)

A função f(2.x) tem metade (1/2) do período de f(x) ---> (2.pi)/2 = pi
A função f(x/2) tem o dobro (2) do período de f(x) ---> 2.(2.pi) = 4.pi

E assim por diante