(UFPA) Vértice da Parábola

Por ocasião da inauguração de um edifício, um promotr de eventos decidiu fazer uso simultâneo das projeções de um jato de água e de um canhão de luz efetuadas a partir de um pequeno prédio vizinho, localizado a 18 metros do edifício novo. O jato será lançado a partir do teto do pequeno prédio ( a 9 metros de altura) e, após executar sua trajetória parabólica, atingirá a base do prédio novo. O canhão de luz, por sua vez, será disparado a partir do chão, da base do pequeno prédio. Seu feixe de luz atravessará exatamente o vértice da ''parábola da água'' e atingirá o topo do novo edifício, que se encontra a 36 metros de altura. A que altura, a partir do solo, o jato de água e o feixe de luz se encontrarão?




(Fiz a imagem no PAINT... então considerem que isso é uma parábola mesmo kkk)

O que fiz: Interpretei a figura como um plano cartesiano. A origem do sistema ficou exatamente no local onde fica o canhão de luz. O feixe de luz descreve uma trajetória retilínea [ f(x) = ax+b ] e o jato de água descreve uma parábola [f(x) = ax²+bx+c]. Encontrei a função do feixe de luz, mas na função da parábola não consegui encontrar ''a'' e nem ''b''. Tentei usar as relações entre raízes e coeficientes misturado com as coordenadas do vértice da parábola, mas não consegui... ajuda!!

Existe uma falha no enunciado:

Faltou o ângulo de lançamento com a horizontal
ou
O lançamento é horizontal e seu desenho está péssimo (kkkkk)

Vou supor a 2ª hipótese (kkkk)

Vou fazer um sistema xOy, porém diferente, para facilitar a explicação:

Canhão de luz na origem
Eixo Y para a esquerda e eixo X para cima.
Depois tombe o desenho para ver os eixos na posição normal.

A parábola tem vértice V(0, -18) e raízes y' = - 9 e y" = + 9

Equação da parábola ----> y = ax² - 18

Para x = 9 ----> y = 0 -----> 0 = a*9² - 18 ----> a = 2/9

Equação da parábola -----> y = (2/9)*x² - 18

Equação da reta do raio de luz ----> passa por O(0, 0) e P(36, -18):

y - 0 = [(-18 - 0)/(36 - 0)]*(x - 0) ----> y = - (1/2)*x

Ponto de encontro ----> (2/9)*x² - 18 = - (1/2)*x ----> 4x² + 9x - 324 = 0

Delta = b² - 4ac ----> D = 9² - 4*4*(-324) ----> D = 5265 ----> \/(D) = 9*\/65

Raiz positiva ---> x = (- 9 + 9*\/65)/2*4 ---> x = 9*(\/65 - 1)/8 ---> x ~= 7,94 m

kkkkk... preciso de um programa para fazer isso, o paint só dá vexame. Essa questão foi retirada de uma apostila sobre função do segundo grau; é a antepenúltima questão, eu já esperava uma questão mais elaborada... mas achei muito estranha. Essa apostila foi o professor da UFPB-Monteiro que passou para seus alunos e blá blá blá... chegou em minhas mãos e não vi solução.

Sem gabarito, falarei com meu amigo. Obrigado mesmo mestre Elcioschin.

Mestre, a resposta é 12 metros. Uma simples análise... veja que a ''função'' do feixe de luz [f(x)=2x] intercepta o vértice da parábola[''função'' que descreve a parábola é g(x)=ax²+bx+9] no vértice desta, logo sendo o valor de g(x)=2x no vértice, mas o ''x'' da função f(x) representa o Xv da parábola também .





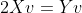
Ai é só substituição! Um colega meu mostrou a resolução de outra pessoa kkkk!


Olhando para a imagem que fiz podemos fazer o seguinte:


Sei que quando x for 18 y será zero..



Ai agora é só substituir e encontrar os coeficientes ''a'' e ''b'' para depois calcular o Yv que dará a altura.