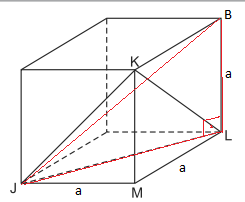
Geometria Espacial Unit Medicina Maceió 2017
2 participantes
Página 1 de 1
Geometria Espacial Unit Medicina Maceió 2017
por fatimacruz16 Ter 02 Jan 2018, 10:39
Considere um cubo cuja diagonal mede 6√3 u.c., como na ilustração. Se V, em u.v., é o volume do tetraedro inscrito no cubo, o valor real de V é? Gabarito: 36.
fatimacruz16- Iniciante
- Mensagens : 26
Data de inscrição : 14/09/2016
Idade : 37
Localização : feira de santana, bahia, brasil
Re: Geometria Espacial Unit Medicina Maceió 2017
por xSoloDrop Ter 02 Jan 2018, 12:29
JB é a diagonal do cubo. Assim, JB = 6√3.
JL é a diagonal do lado do cubo. Assim, JL = a√2.
No triângulo JBL:
JB² = BL² + JL²
(6√3)² = a² + (a√2)²
108 = a² + 2a²
a = 6
O volume do tetraedro é dado por:
V = [(JM.ML/2).KM]/3
V = a³/6
V = 6³/6
V = 36
xSoloDrop- Fera
- Mensagens : 492
Data de inscrição : 23/03/2015
Idade : 26
Localização : Araçatuba SP
Re: Geometria Espacial Unit Medicina Maceió 2017
por fatimacruz16 Ter 02 Jan 2018, 18:04
Muito obrigada!
fatimacruz16- Iniciante
- Mensagens : 26
Data de inscrição : 14/09/2016
Idade : 37
Localização : feira de santana, bahia, brasil
Tópicos semelhantes» Geometria Plana-Unit Medicina 2017.1 Maceió
» UNIT-MACEIÓ MEDICINA 2016
» unit maceió 2017.2
» unit maceió 2017.2
» unit maceió 2017.2
» UNIT-MACEIÓ MEDICINA 2016
» unit maceió 2017.2
» unit maceió 2017.2
» unit maceió 2017.2
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
