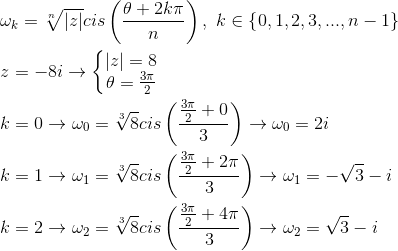Números Complexos - Representação gráfica
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1

Augusto H.- Mestre Jedi

- Mensagens : 509
Data de inscrição : 22/03/2017
Idade : 25
Localização : Porto Alegre
 Re: Números Complexos - Representação gráfica
Re: Números Complexos - Representação gráfica
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8526
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Números Complexos - Representação gráfica
Re: Números Complexos - Representação gráfica
O passo de somar +i que acho confuso, por alguma maneira achei que deveria calcular 3 raízes de i....
Mas compreendi a resolução, eu que estava complicando hehe. Obrigado Giovana!!!
Mas compreendi a resolução, eu que estava complicando hehe. Obrigado Giovana!!!

Augusto H.- Mestre Jedi

- Mensagens : 509
Data de inscrição : 22/03/2017
Idade : 25
Localização : Porto Alegre
 Re: Números Complexos - Representação gráfica
Re: Números Complexos - Representação gráfica
De nada. Augusto, o número complexo w=i já está na sua forma natural, a+bi, com a=0 e b=1, sendo assim, não é necessário calcular a raiz de i. O número complexo √(-8i), por sua vez, não está na sua forma natural, motivo pelo qual extrai-se as suas raízes complexas para que a posterior soma seja feita. Imagine que o número complexo z=i+√(-8i) esteja em "função" das raízes de √(-8i), daí a notação zk=i+ωk, em que o i seria uma "constante". Esse foi mais ou menos raciocínio que eu usei para resolver o exercício.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8526
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Números Complexos - Representação gráfica
Re: Números Complexos - Representação gráfica
A claro!!! Ótima explicação, abraços!

Augusto H.- Mestre Jedi

- Mensagens : 509
Data de inscrição : 22/03/2017
Idade : 25
Localização : Porto Alegre

Willian Honorio- Matador

- Mensagens : 1271
Data de inscrição : 28/04/2016
Idade : 27
Localização : São Paulo
 Re: Números Complexos - Representação gráfica
Re: Números Complexos - Representação gráfica
Boa informação adicional, Willian. Obrigada.
____________________________________________
Charlotte de Witte - Universal Nation

Giovana Martins- Grande Mestre

- Mensagens : 8526
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Tópicos semelhantes
Tópicos semelhantes» Números Complexos - (representação gráfica)
» Numeros complexos - representação grafica
» Complexos (representação gráfica)
» Representação geométrica dos números complexos
» (MACK) - representação números complexos
» Numeros complexos - representação grafica
» Complexos (representação gráfica)
» Representação geométrica dos números complexos
» (MACK) - representação números complexos
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos