Soma de Vetores

Dois vetores, 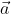 e 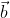, de módulos respectivamente iguais a 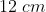e 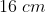, pertencem ao mesmo plano. Sendo 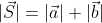, o valor do 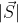não pode ser

A)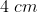
B)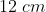
C)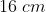
D)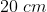
E)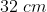

O gabarito está como E)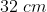

Mas eu tenho algumas dúvidas com relação a essa questão. Eu pensei assim:
Existem quatro casos possíveis para esses dois vetores,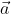  e 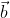, que são os seguintes:
Caso 1:
Eles são paralelos e com o mesmo sentido, portanto, o valor do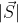  será igual a soma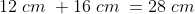
Caso 2: 
Eles são paralelos e com sentidos opostos, portanto, o valor do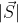 será igual a diferença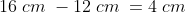 
Caso 3:
Eles são perpendiculares entre si, portanto, o valor do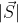 será igual a 
Caso 4:
Eles formam um ângulo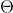  qualquer, e, por conhecimentos de trigonometria, podemos dizer que esse 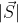é menor que a soma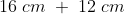
Ou seja, é verdade que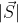 é diferente de 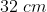, mas também deveria ser verdade que é diferente d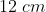e  e 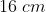. Quero dizer, o 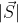não pode assumir esses valores, então a questão ficaria com mais de uma alternativa certa.
Gostaria que alguém me respondesse se eu pensei da maneira correta e a questão está mal estruturada ou se eu cometi algum deslize no meu raciocínio.
Agradeço toda e qualquer sugestão que tenha como fim o melhoramento do meu raciocínio.

Na verdade você pode inclinar os vetores usando valores menos óbvios.
Você só levou em consideração os casos mais óbvios, quando os vetores são perpendiculares, paralelos, etc... Lembre que eles podem fazer qualquer ângulo entre 0º e 360º. O maior valor possível é quando eles é quando o ângulo entre eles é 0º, logo a soma entre eles designa o maior valor possível do vetor resultante entre eles (12 + 16 cm).

SergioEngAutomacao escreveu:Na verdade você pode inclinar os vetores usando valores menos óbvios.
Você só levou em consideração os casos mais óbvios, quando os vetores são perpendiculares, paralelos, etc... Lembre que eles podem fazer qualquer ângulo entre 0º e 360º. O maior valor possível é quando eles é quando o ângulo entre eles é 0º, logo a soma entre eles designa o maior valor possível do vetor resultante entre eles (12 + 16 cm).

Claro, amigo. Obrigado.
O que acontece é que eu supus esse valor máximo (Caso 1), portanto, eles poderiam assumir esse valor, mas a questão nem colocou ele nas alternativas.
Em relação aos outros valores do ângulo , eu pensei o seguinte:
Como são dois vetores, é possível fechar um triângulo com eles dois e a resultante da soma deles, e o módulo do vetor soma será, necessariamente, menor que a soma dos dois outros lados, porque a soma de dois lados de um triângulo é menor que o outro lado.
O problema que eu enfrentei na questão foi que eu descobri que ela não poderia assumir o valor da alternativa E), mas pelos meus cálculos ela também não poderia assumir os valores das alternativas B) e C), e portanto, a questão estaria mal formulada ou meu raciocínio estaria errado. 

você pode formar dois triângulos isósceles com 12cm, 12cm e 16cm de medidas de lado e um outro com 16cm, 16cm e 12cm de medidas. O que prova que é possível inclinar os vetores 12cm e 16cm de modo a atingir os valores de comprimento de vetor de 12cm e 16cm.
Não compreendi a sua dúvida ainda.

SergioEngAutomacao escreveu:você pode formar dois triângulos isósceles com 12cm, 12cm e 16cm de medidas de lado e um outro com 16cm, 16cm e 12cm de medidas. O que prova que é possível inclinar os vetores 12cm e 16cm de modo a atingir os valores de comprimento de vetor de 12cm e 16cm.
Não compreendi a sua dúvida ainda.

Eu fiz uma confusão em relação aos lados do triângulo, mas pensando bem, isso que você falou faz todo sentido. Obrigado

O exercício é simples: a, b e S formam um triângulo ou são paralelos, então



nas alternativas só há um valor fora do intervalo.