UEM PR-2016
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
UEM PR-2016
por Alexandre_Becker Ter 11 Jul 2017, 22:26
Seja m um número real. Em relação à função dada por f(x) = mx²+4mx+(m+1), é correto afirmar que
01) é uma função quadrática para todo m real.
02) para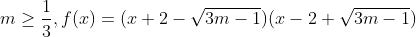
04) para todo m < 0 , o gráfico é uma parábola com concavidade para baixo e com duas raízes reais.
08) a função é positiva para todo x real, sempre que 0 < m<1/3
16) para m = 2 , a função é negativa para todo x real.
01) é uma função quadrática para todo m real.
02) para
04) para todo m < 0 , o gráfico é uma parábola com concavidade para baixo e com duas raízes reais.
08) a função é positiva para todo x real, sempre que 0 < m<1/3
16) para m = 2 , a função é negativa para todo x real.
- Gabarito:
- 12
Última edição por Alexandre_Becker em Qua 12 Jul 2017, 08:07, editado 1 vez(es)
Alexandre_Becker- Iniciante
- Mensagens : 37
Data de inscrição : 08/04/2017
Idade : 24
Localização : Maringá, Paraná Brasil
Re: UEM PR-2016
por Elcioschin Ter 11 Jul 2017, 22:55
f(x) = m.x² + 4.m.x + (m + 1)
∆ = (4.m)² - 4.m.(m + 1) ---> ∆ = 12.m² - 4.m ---> ∆ = 4.(3.m² - m) --->
Para a função ser real ---> ∆ ≥ 0 ---> 3.m² - m ≥ 0 ---> Raízes m = 0 e m = 1/3
Devemos ter m ≤ 0 ou m ≥ 1/3
01) Falsa ---> Para m = 0 ---> f(x) = 1 (não é função quadrática)
02) Faça um teste
04) Verdadeira (vide acima)
08 ) não deu para entender a frase: está incompleta.
16) Para m = 2 ---> m > 1/3 --> f(x) > 0 ---> Falsa
∆ = (4.m)² - 4.m.(m + 1) ---> ∆ = 12.m² - 4.m ---> ∆ = 4.(3.m² - m) --->
Para a função ser real ---> ∆ ≥ 0 ---> 3.m² - m ≥ 0 ---> Raízes m = 0 e m = 1/3
Devemos ter m ≤ 0 ou m ≥ 1/3
01) Falsa ---> Para m = 0 ---> f(x) = 1 (não é função quadrática)
02) Faça um teste
04) Verdadeira (vide acima)
08 ) não deu para entender a frase: está incompleta.
16) Para m = 2 ---> m > 1/3 --> f(x) > 0 ---> Falsa
Elcioschin- Grande Mestre
- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: UEM PR-2016
por Alexandre_Becker Qua 12 Jul 2017, 08:09
Não sei porque a 08 nao saiu na hora de enviar a questão, mas de qualquer jeito sua explicação responde essa alternativa, obrigado!
Alexandre_Becker- Iniciante
- Mensagens : 37
Data de inscrição : 08/04/2017
Idade : 24
Localização : Maringá, Paraná Brasil
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
