Perímetro

Obtenha o perímetro do trapézio isósceles, com ângulo de 60º, que está circunscrito a um círculo de 12 cm de diâmetro .



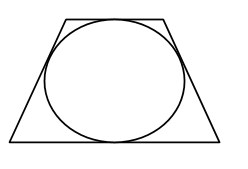
Como eu faço nesses casos ? acho o comprimento da circunferência primeiro ?

nanzinho12 escreveu:Obtenha o perímetro do trapézio isósceles, com ângulo de 60º, que está circunscrito a um círculo de 12 cm de diâmetro .



Como eu faço nesses casos ? acho o comprimento da circunferência primeiro ?

Bom dia, nanzinho12.

Nessa figura, as somas dos lados opostos do trapézio são iguais entre si.
Clique e veja:

V=https://www.google.com.br/search?q=trapezio+circunscrito+a+um+circulo&biw=933&bih=447&tbm=isch&imgil=LiYRqCrA4lX2GM%253A%253By64mSL4EPd9vPM% 

Como os ângulos agudos da base medem 60°, faça o seguinte:
Identifique os vértices do trapézio, a partir do vértice inferior esquerdo, e em sentido horário, marque-os com as letras A, B, C e D.
A partir do vértice superior esquerdo (B), baixe uma perpendicular à base AD, lembrando que sua medida será igual ao diâmetro do círculo inscrito (12).
Identifique o pé dessa perpendicular pela letra E.
Como o ângulo BAE mede 60°, o ângulo ABE, seu complementar, deve medir 30°.
AE/AB = sen 30° = 1/2
AB = 2.AE

Fazendo-se, então, AE=x, vem:
AE = x
AB = 2x

Assim, no triângulo retângulo AEB, temos:
(AB)² = (12)² + (AE)²
(2x)² = 144 + x²
4x² - x² = 144
3x² = 144
x² = 144/3 = 48
x = √48
x = 4√3 

Logo,
AB = 2x = 2.4√3 = 8√3 cm

Aplicando-se a propriedade de que as somas dos lados opostos do trapézio são iguais, vem:
AB + CD = BC + AD

Sendo CD=AB, fica:
AB + AB = BC + AD
2.AB = BC + AD = 2.8√3 = 16√3 cm

E assim, obtemos o perímetro do referido trapézio como sendo igual a:
2*16√3 = 32√3 cm





Um abraço.