Em função dos ângulos

No triângulo abaixo,E e D são pontos d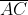e e 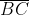, respectivamente. é a bissetriz do ângulo e é a bissetriz do ângulo .A medida do ângulo em função dos ângulos e é: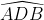

a)
b)
c)
d)
e)

Seja T o ponto de encontro entre AF e EB.
Seja W o ponto de enconro entre AD e EB.
Seja γ o ângulo AÊB
Seja α o ângulo EÂB
Seja ∆ o ângulo ADB
Seja b o ângulo DBE
Seja ∂ o ângulo AFB.

Analisando o triângulo DWB, temos que o ângulo externo em W é igual à soma dos ângulos ∆ e b e analisando o triângulo AEW, olhando para o ângulo externo em W, temos que esse mesmo ângulo é igual à soma de α e γ.

∆ + b = α + γ
α - b = ∆ - γ (I)


Analisando o triângulo TFB, temos que o ângulo externo em T é igual à soma dos ângulos ∂ e /2. No mesmo ponto T, vamos analisar o triângulo AET e vemos que o ângulo externo em T é igual a α/2 mais γ. Logo, podemos escrever a equação:

∂ + b/2 = α/2 + γ

∂ = (α - b)/2 + γ (II)

Substituindo (I) em (II), temos:
∂ = (∆ - γ )/2 + γ
∂ = (∆ + γ )/2 ou seja:

AFB= (ADB+AEB)/2


letra C