Teoria dos números (divisibilidade)

Encontre o número de inteiros n tais que:
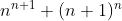 é divisível por 3.


Creio que seja necessário utilizar a fatoração de x^n + y^n.

Grato desde já.

John von Neumann jr escreveu:Encontre o número de inteiros n tais que:
 é divisível por 3.


Creio que seja necessário utilizar a fatoração de x^n + y^n.

Grato desde já.

Boa tarde, John.

Encontrei n=1:

1² + 2¹ = 1 + 2 = 3, sendo que 3|3 obviamente. 

Será que existe(m) outro(s)??


Um abraço.

Boa tarde, Ivo.

Encontrei no pir2 um tópico que trata desta mesma questão:
https://pir2.forumeiros.com/t61880-teoria-dos-numeros-divisibilidade

No entanto não sei se está correto.

John von Neumann jr escreveu:Boa tarde, Ivo.

Encontrei no pir2 um tópico que trata desta mesma questão:
https://pir2.forumeiros.com/t61880-teoria-dos-numeros-divisibilidade

No entanto não sei se está correto.

Boa noite, John.

Creio que seu problema deva ser o mesmo dessa questão, que coloque limites para n (maior que 1000 e menor que 8000):

http://poti.impa.br/uploads/material_teorico/82r7a10d1jocg.pdf

Consegui compreender a resolução que está no link que você postou agora:

Encontre o número de inteiros n tais que:

1. 1000 < n < 8000.

2. nⁿ⁺¹ + (n+1)ⁿ é divisível por 3.

É de um material, mas lá não tem respostas nem resolução. Alguém pode ajudar? '-'

jplogininiciante

Mensagens :  7
Data de inscrição :  12/03/2013
Idade :  19
Localização :  Fortaleza


Re: Teoria dos números - divisibilidade

 por wbao em Qui Jan 09, 2014 2:28 pm

Não sei se tá certo,mas fiz assim(também quero a resposta certa dela):
Os possíveis restos de n por 3 são 0,1 e 2. Seja n^(n+1)+(n+1)^n = N
*Se n deixa resto 0 na divisão por 3 então o resto da divisão por 3 de N será (0+1)/3, a mesma coisa que resto 1.
*Se n deixa resto 1 na divisão por 3, N deixa resto (1+2^n)/3 . Dessa forma N será divisível por 3 somente se n for ímpar(Lembre da fatoração X^n + Y^n).
* Se n deixa resto 2 na divisão por 3, N deixará resto (2³ + 3^n)/3. Como 3 divide 3^n, o resto será o mesmo da divisão  de 2³ por 3 que é 2.

Logo N será divisível por 3 quando n for ímpar e deixar resto 1 na divisão por 3. Logo n é da forma 2k +1, onde k é 3q( q =  1,2,3,4...),pois n tem que ser ímpar e múltiplo de 3. Logo n= 6q+1; Como 1000< n <8000, o primeiro número que satisfará as condições é o 1003=6.167 + 1; e o último é 7999 = 6.1333+1; Logo q varia de 167 a 1333, e nesse intervalo há 133-167 +1 = 1667 números.
Logo a resposta é 1667.
Se essa não for a resposta me diga tá? Pois estou respondendo esse mesmo material(acho) e não sei a resposta.
Fica com Deus
----------------------------------------------------------------------------------------------
Pela explicações dadas acima, n deverá ser ímpar e deixar resto 1 quando dividido por 3. Assim, para ser ímpar, n deve ter formato igual a 2k+1 e ser divisível por 3. Isso faz com que n seja igual a 6q+1, ou seja, seus valores deverão ser: 1,7,13,19,25,...

Como n deve estar situado entre 1000 e 8000, e 1000/6 = 166,666..., então o menor valor possível para n deverá ser esse valor arredondado para mais (para que 6.167 + 1 seja maior que 1000).

Quanto ao maior valor, temos que 8000/6 = 1333,333, o maior valor de n deverá ser esse valor, arredondado para menos (para que 6.1333 + 1 seja menor que 8000).
Assim, a quantidade de números n dentre 1000 e 8000 será igual a:
1333 - 167 + 1 = 1167.

Explicando melhor:
Menor valor para N = (167)¹⁶⁸ + (168)¹⁶⁷
Maior valor para N = (1333)¹³³⁴ + (1334)¹³³³



Um abraço.

Muito obrigado!