Teoria dos números (divisibilidade)

Encontre o resto da divisão 37^10 − 1 por 11.
Cheguei em que: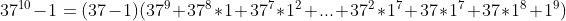  , entretanto não consigo avançar.

John von Neumann jr escreveu:Encontre o resto da divisão 37^10 − 1 por 11.
Cheguei em que:  , entretanto não consigo avançar.

Bom dia, John.

Encontremos os restos das sucessivas potências de 37, quando divididas por 11:
resto de (37)¹/11 = 4
resto de (37)²/11 = 5
resto de (37)³/11 = 9
resto de (37)⁴/11 = 3
resto de (37)⁵/11 = 1
resto de (37)⁶/11 = 4 (e a partir daqui recomeça: 4,5,9,3,1 4,5,9,3,1 ...)

Como se deve diminuir 1 de cada uma das potências, fica:
resto de (37)¹/11 - 1 = 3
resto de (37)²/11 - 1 = 4
resto de (37)³/11 - 1 = 8
resto de (37)⁴/11 - 1 = 2
resto de (37)⁵/11 - 1 = 0

Assim, os restos que as potências sucessivas de 37, –1, quando divididas por 11, são:
3,4,8,2,0   3,4,8,2,0   ...

Como o expoente de 37 é igual a 10, que comporta 2 vezes inteiras (37)⁵, temos que:
resto de 10/5 = 0

Resto 0 corresponde às potências de 37 múltiplas de 5; portanto, podemos afirmar:
Resto de (37)¹º - 1 por 11 = 0



Um abraço.

Como o senhor encontrou os restos nas divisões?Tenho que calcular 37^1,37^2,37^3...?

Desde já, muito obrigado!

John von Neumann jr escreveu:Como o senhor encontrou os restos nas divisões?Tenho que calcular 37^1,37^2,37^3...?

Desde já, muito obrigado!

Boa tarde, John.

Não, tem um modo mais fácil, veja:
(r) 37/11 _____________________ = 4
(r) 37²/11 = (r) 4*4/11 = (r) 16/11 = 5
(r) 37³/11 = (r) 5*4/11 = (r) 20/11 = 9
(r) 37⁴/11 = (r) 9*4/11 = (r) 36/11 = 3
(r) 37⁵/11 = (r) 3*4/11 = (r) 12/11 = 1

Ou seja, vai multiplicando o primeiro resto (4) por 4, como se fosse encontrar o resto de 4²/11, de 4³/11, de 4⁴/11 e de 4⁵/11 (os resultados serão os mesmos que se fizesse:
(r) 37²/11; (r) 37³/11; etc.




Um abraço.

Tinha esquecido disso.
Muito obrigado!