Questão sobre ângulos de duas retas
3 participantes
Página 1 de 1
 Questão sobre ângulos de duas retas
Questão sobre ângulos de duas retas
Seja E(-2;3) o centro de um quadrado ABCD. Sabendo que a reta AB tem equação
x-2y+3=0, determine as equações das retas que contêm as diagonais do quadrado.
R: 3x-y+9=0 e x+3y-7=0
x-2y+3=0, determine as equações das retas que contêm as diagonais do quadrado.
R: 3x-y+9=0 e x+3y-7=0
vandersonbelmont- Recebeu o sabre de luz

- Mensagens : 118
Data de inscrição : 12/11/2015
Idade : 29
Localização : Rio de Janeiro
 Re: Questão sobre ângulos de duas retas
Re: Questão sobre ângulos de duas retas
Vou fazer parte e você completa
1) Desenhe sistema xOy e poste, em escala, ponto E(-2;3) e reta AB: x - 2y + 3 = 0
2) Por E trace uma reta perpendicular à reta AB, no ponto M. Este ponto M é o ponto médio do lado AB, logo, a distância EM é igual à metade do lado do quadrado
y = (1/2).x + 3/2 ---> tgα = 1/2 (α = ângulo da reta com o eixo x)
EM = |1.(-2) - 2.(3) + 3|/√[1² + (-2)²] ---> EM = √5 ---> AM = √5 ---> AB = 2.√5
BC = CD = DA = 2.√5 --> d² = AB² + BC² --> d² = 40 --> d = 2.√10 ---> diagonal
No triângulo retângulo EMA ---> tg(EÂM) = tg45º ---> tgθ = 1
Reta AC ---> m = tg(θ + α) = tg(45º + α) = (tg45º + tgα)/(1 - tg45º.tgα) --->
m = (1 + 1/2)/[1 - 1.(1/2)] ---> m = 3
Equação de AC ---> y - yE = m.[x - xE] ---> y - 3 = 3.[x - (-2)] ---> 3x - y + 9 = 0
Para calcular a equação de BD ---> passa por E(-2;3) e é perpendicular a AC
1) Desenhe sistema xOy e poste, em escala, ponto E(-2;3) e reta AB: x - 2y + 3 = 0
2) Por E trace uma reta perpendicular à reta AB, no ponto M. Este ponto M é o ponto médio do lado AB, logo, a distância EM é igual à metade do lado do quadrado
y = (1/2).x + 3/2 ---> tgα = 1/2 (α = ângulo da reta com o eixo x)
EM = |1.(-2) - 2.(3) + 3|/√[1² + (-2)²] ---> EM = √5 ---> AM = √5 ---> AB = 2.√5
BC = CD = DA = 2.√5 --> d² = AB² + BC² --> d² = 40 --> d = 2.√10 ---> diagonal
No triângulo retângulo EMA ---> tg(EÂM) = tg45º ---> tgθ = 1
Reta AC ---> m = tg(θ + α) = tg(45º + α) = (tg45º + tgα)/(1 - tg45º.tgα) --->
m = (1 + 1/2)/[1 - 1.(1/2)] ---> m = 3
Equação de AC ---> y - yE = m.[x - xE] ---> y - 3 = 3.[x - (-2)] ---> 3x - y + 9 = 0
Para calcular a equação de BD ---> passa por E(-2;3) e é perpendicular a AC

Elcioschin- Grande Mestre

- Mensagens : 73162
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Questão sobre ângulos de duas retas
Re: Questão sobre ângulos de duas retas
Seja l o lado do quadrado ABCD. Perceba que a distância do ponto E ao lado do quadrado é l/2.
Assim, temos que :
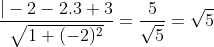
Como esta distância corresponde à metade, seu dobro é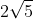
Da equação da reta que contém o lado AB podemos deduzir que o quadrado está rotacionado, uma vez que seus lados não formam noventa graus com os eixos. Assim, vamos rotacionar este quadrado para conseguir esta propriedade: ser normal aos eixos.
Perceba que o vetor diretor da reta dada é (2,1), assim, como na figura:

Então, considere a matriz de rotação:
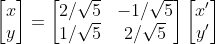 , onde x' e y' representam as novas coordenadas após a rotação.
, onde x' e y' representam as novas coordenadas após a rotação.
Então,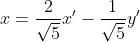 e
e 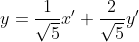 . Substituindo x e y na reta dada, temos:
. Substituindo x e y na reta dada, temos:
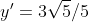 . Esta é a nova equação da reta após rotação. Novamente, o fato de não conter nenhum valor para x é uma comprovação de que a reta forma noventa graus com o eixo y e é paralela ao eixo x.
. Esta é a nova equação da reta após rotação. Novamente, o fato de não conter nenhum valor para x é uma comprovação de que a reta forma noventa graus com o eixo y e é paralela ao eixo x.
Podemos também transladar o quadrado para a origem, já que temos o centro dele. Isto é, colocar o centro como a origem O = (0,0).
Assim, substituindo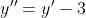 na reta que obtemos, segue:
na reta que obtemos, segue:
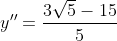 , que é a equação da reta dada rotacionada e transladada.
, que é a equação da reta dada rotacionada e transladada.
Como já encontramos que l/2 é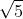 , o ponto B do quadrado tem coordenadas:
, o ponto B do quadrado tem coordenadas: 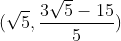 .
.
Refletindo este ponto entorno da reta x=0, temos que o ponto A tem coordenadas: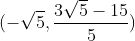
Como o centro é (0,0), porque transladamos, agora temos dois pontos das retas AO e BO.
Então podemos determiná-las:
O vetor diretor de BO é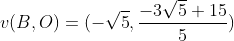 .
.
Logo, a reta BO tem equação :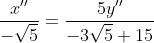
Da mesma forma, temos que o vetor diretor de de AO é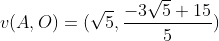 .
.
Logo, AO tem equação: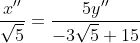
Agora, tão-somente resta realizar todo o processo inverso e encontrar as retas AO e BO nas coordenadas originais.
Primeiramente, vamos transladar entorno do ponto E(-2,3), ao substituir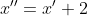 e
e 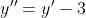 .
.
Assim, as retas ficam:
AO: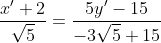 e BO:
e BO: 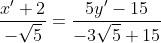 .
.
Agora, vamos rotacionar tais retas pelo mesmo ângulo que rotacionamos anteriormente, só que em sentido contrário, a fim de voltar o quadrado à disposição original.
A matriz de rotação inversa é dada como a seguir, para o mesmo ângulo:
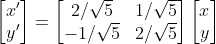 , de onde obtemos que
, de onde obtemos que 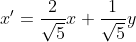 e
e 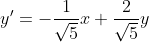
Substituindo em cada uma das retas dadas, obtemos que:
Assim, temos que :
Como esta distância corresponde à metade, seu dobro é
Da equação da reta que contém o lado AB podemos deduzir que o quadrado está rotacionado, uma vez que seus lados não formam noventa graus com os eixos. Assim, vamos rotacionar este quadrado para conseguir esta propriedade: ser normal aos eixos.
Perceba que o vetor diretor da reta dada é (2,1), assim, como na figura:

Então, considere a matriz de rotação:
Então,
Podemos também transladar o quadrado para a origem, já que temos o centro dele. Isto é, colocar o centro como a origem O = (0,0).
Assim, substituindo
Como já encontramos que l/2 é
Refletindo este ponto entorno da reta x=0, temos que o ponto A tem coordenadas:
Como o centro é (0,0), porque transladamos, agora temos dois pontos das retas AO e BO.
Então podemos determiná-las:
O vetor diretor de BO é
Logo, a reta BO tem equação :
Da mesma forma, temos que o vetor diretor de de AO é
Logo, AO tem equação:
Agora, tão-somente resta realizar todo o processo inverso e encontrar as retas AO e BO nas coordenadas originais.
Primeiramente, vamos transladar entorno do ponto E(-2,3), ao substituir
Assim, as retas ficam:
AO:
Agora, vamos rotacionar tais retas pelo mesmo ângulo que rotacionamos anteriormente, só que em sentido contrário, a fim de voltar o quadrado à disposição original.
A matriz de rotação inversa é dada como a seguir, para o mesmo ângulo:
Substituindo em cada uma das retas dadas, obtemos que:

maico33LP- Matador

- Mensagens : 465
Data de inscrição : 25/07/2013
Idade : 28
Localização : Campinas
 Tópicos semelhantes
Tópicos semelhantes» Ângulos entre duas retas
» Questão sobre RETAS
» Sobre Angulos e Retas paralelas
» Questão sobre retas
» Questão sobre Retas
» Questão sobre RETAS
» Sobre Angulos e Retas paralelas
» Questão sobre retas
» Questão sobre Retas
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












