Média Aritmética

Quatro números pares consecutivos são removidos do conjunto 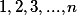. Se a média aritmética dos números restantes é 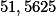, determine o valor de  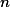e quais são os números removidos:
Respostas:
n=100
22,24,26 e 28

joaowin3 escreveu:Quatro números pares consecutivos são removidos do conjunto . Se a média aritmética dos números restantes é , determine o valor de  e quais são os números removidos:
n=100
22,24,26 e 28

Boa tarde, João.

51,5625 = 51 + 0,5625

0,5625 = 5625/10000 = 9/16
51 + 9/16 = (51*16 + 9)/16 = 825/16

Quantidade de números que sobrou da série 1,2,3,...,n = n - 4.
51,5625 * (n-4) = 825/16 * (n-4).

Como 825 é primo com 16, necessariamente (n-4) deverá ser divisível por 16, ou seja, deverá ser múltiplo de 16; logo, podemos escrever:
n-4 = 16k
n = 4 + 16k (com k≥1)

Assim, fazendo k=1,2,3,..., os possíveis valores de n deverão ser 20, 36, 52,...
A soma desses valores de k, por sua vez, irá seguir segundo o valor obtido na fórmula da soma dos termos de uma PA, a saber:
Para n=20 → S20 = (1+20).20/2 = 21*20 = 210
Para n=36 → S36 = (1+36).36/2 = 37*18 = 666
etc.

Aplicando-se n=4+16k na fórmula do soma dos termos de uma PA, vem:
Sn = (a1 + an)*n/2
Sn = (1 + 4+16k)(4+16k)/2
Sn = (5+16k)(4+16k)/2 = 128.k² + 72.k + 10

Esta soma deverá ser maior que 825*k ; portanto, vem:
128.k² + 72.k + 10 > 825.k
128.k² - 753.k + 10 > 0

Calculando as raízes k do primeiro membro, fica:
k' = 5,8671875
k" = 0,015625

Assim, para a desigualdade supra ser maior que zero, seus valores de k deverão ser:

0,015625 > k > 5,8671875

Como k deve ser inteiro, teremos que ter:
k > 5,8671875
k ≥ 6

Considerando k=6, fica:
n = 4 + 16k
n = 4 + 16*6 = 4 + 96
n = 100

A soma da série de 1 a n (=1 a 100) é:
S100 = (1+100)*100/2 = 101*50 = 5050

A soma dos 96 números que restaram deverá ser igual a:
51,5625 * 96 = 4950

Então os 4 números pares que foram retirados devem somar:
5050 - 4950 = 100

Determinando o menor desses 4 números pares:
x + x+2 + x+4 + x+6 = 100
4x + 12 = 100
4x = 100 - 12 = 88
x = 88/4
x = 22

Finalizando, os 4 números pares são:
22, 24, 26 e 28



Um abraço.

Ivomilton, o n=100 é uma das respostas da questão, não um dado dela.

joaowin3 escreveu:Ivomilton, o n=100 é uma das respostas da questão, não um dado dela.

Boa noite, joaowin3.

Entendi. Editei e refiz a resolução.
Agora está correta.



Tenha um abençoado final de semana!