Ponto e Reta

(IME-70) Estabeleça as equações das retas que distam 10 unidades da origem e que contém o ponto (5,10).
a)3x-2y=20 e y=-6
b)3x+4y=60 e x+2=0
c)x-y-2 e y=10
d)4x+3y=50 e y=10
e)4x+2y=50 e x+2y=10

Gabarito: D

Distância de um ponto à uma reta:

Portanto, se dista 10 unidades, temos então que:

Agora, se a reta contém o ponto (5, 10), então:

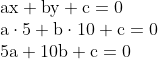
Agora, temos um sistema:

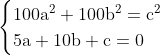
Pra resolver esse sistema, uma maneira é fazer o seguinte:

E dividimos um pelo outro:

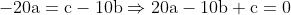
Agora, temos duas equações lineares(sem termos quadraticos para complicar as equações):


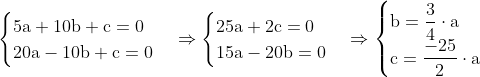
Então, para lidarmos com somente inteiros, vamos chamar a=4, então:


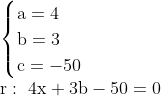
Essa é uma das retas, que indica somente a D como alternativa correta. Não obtivemos a outra resposta (y=10) pois durante a passagem que dividimos:

Consideramos que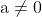 , o que indicaria que não estamos tratando de retas horizontais, sendo estas possiveis.

Uma outra forma:

- família de retas que passam pelo ponto ( 5, 10 )

y - 10 = m*( x - 5 )

y = m*x - 5*m + 10


- retas tangentes à circunferência x² + y² = 100 e que passam pelo ponto ( 5, 10 ):

x² + y² = 100

y = m*x - 5*m + 10

x² + ( m*x - 5*m + 10 )² = 100

x² + m*x² - 10*m²*x + 20*m*x + 25*m² - 100*m + 100 - 100 = 0

( 1 + m² )*x² - ( 10*m² - 20*m )*x + 25*m² - 100*m = 0

......( 10*m² - 20*m ) (+/-)\/[ (10*m² - 20*m )² - 4*( 1 + m² )*( 25*m² - 100*m ) ]
x = -----------------------------------------------------------------------------------------------------
.............................................. 2*( 1 + m² )


para que ocorra tangência devemos ter o discriminante igual a zero:

( 10*m² - 20*m )² - 4*( 1 + m² )*( 25*m² - 100*m ) = 0

300*m² + 400*m = 0

raízes :m = 0 ou m = - 4/3

assim:

para m = 0 -> y = 0*x - 0 + 10 -> y = 10

para m = - 4/3

y = - ( 4/3 )*x - 5*( - 4/3 ) + 10

3*y = - 4*x + 50

4*x + 3*y - 50 = 0