Progressão Geométrica - IDECAN
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Progressão Geométrica - IDECAN
Progressão Geométrica - IDECAN
Bom dia, pessoal!
Alguém me ajuda a resolver essa questão, por favor?
O produto dos quatro termos de uma progressão geométrica de números reais, cuja razão é um número inteiro, é 16. A soma dos dois termos centrais é 5. Logo, a soma dos dois últimos termos é:
A) 16.
B) 20.
C) 21.
D) 24
Alguém me ajuda a resolver essa questão, por favor?
O produto dos quatro termos de uma progressão geométrica de números reais, cuja razão é um número inteiro, é 16. A soma dos dois termos centrais é 5. Logo, a soma dos dois últimos termos é:
A) 16.
B) 20.
C) 21.
D) 24
andrea_mt- Iniciante
- Mensagens : 5
Data de inscrição : 26/02/2016
Idade : 34
Localização : Campina Grande, PB
 Re: Progressão Geométrica - IDECAN
Re: Progressão Geométrica - IDECAN
PG ---> a, a.q, a.q², a.q³
a.(a.q).(a.q²).(a.q³) = 16 ---> a4.q6 = 4² ---> a².q³ = 4 ---> a.q3/2 = 2 ---> a = 2/q3/2
a.q + a.q² = 5 ---> (2/q3/2).q + (2/q3/2).q² = 5 ---> 2/q + 2.q = 5 ---> 2.q² - 5.q + 2 = 0 ---> Raízes: q = 2 e q = 1/2
Complete
a.(a.q).(a.q²).(a.q³) = 16 ---> a4.q6 = 4² ---> a².q³ = 4 ---> a.q3/2 = 2 ---> a = 2/q3/2
a.q + a.q² = 5 ---> (2/q3/2).q + (2/q3/2).q² = 5 ---> 2/q + 2.q = 5 ---> 2.q² - 5.q + 2 = 0 ---> Raízes: q = 2 e q = 1/2
Complete

Elcioschin- Grande Mestre

- Mensagens : 73182
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Progressão Geométrica - IDECAN
Re: Progressão Geométrica - IDECAN
Pg: (a1,a2,a3,a4)
a2 + a3=5
a1.q + a2.q²=5
Produto:
^{2}=(a1.an)^{n})
^{2}=(a1.a4)^{4})
![\sqrt[4]{(4)^{4}}=(a1.a4)](https://latex.codecogs.com/gif.latex?\sqrt[4]{(4)^{4}}=(a1.a4))
)
=a1^{2}.q^{3})
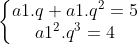
Resolvendo o sistema por substituição, teremos:
a1(q+q²)=5
a1=5/(q+q²) Substituindo na equação ''debaixo'' do sistema, vem:
^{2}}.q^{3}=4)
25q³ = 4(q+q²)²
25q³ = 4q² + 4q4 + 8q³
-4q4 + 17q³ - 4q² = 0
q²( -4q² + 17q -4)=0
q²=0 ou -4q²+17q -4=0
Resolvendo a segunda equação acima por Báskhara, você chegará em duas raízes: q1=4 e q2=1/4. Mas como o enunciado diz que a razão da PG é um número inteiro, logo a sua razão dentre as raízes da equação é 4. Com isso basta substituir o valor de q em alguma das equações do sistema e você chegará por puro algebrismo no valor de a1, que é 1/4.
a1=5/(q+q²)=5(4+4²)=5/20=1/4
Com isso, você descobre os valores de a3 e a4:
a3=a1.q²=1/4.4²=4
a4=a1.q³=1/4 .4³=16
a3+ a4=4 + 16=20
Assim, o valor da soma de a3 e a4 é 20.
a2 + a3=5
a1.q + a2.q²=5
Produto:
Resolvendo o sistema por substituição, teremos:
a1(q+q²)=5
a1=5/(q+q²) Substituindo na equação ''debaixo'' do sistema, vem:
25q³ = 4(q+q²)²
25q³ = 4q² + 4q4 + 8q³
-4q4 + 17q³ - 4q² = 0
q²( -4q² + 17q -4)=0
q²=0 ou -4q²+17q -4=0
Resolvendo a segunda equação acima por Báskhara, você chegará em duas raízes: q1=4 e q2=1/4. Mas como o enunciado diz que a razão da PG é um número inteiro, logo a sua razão dentre as raízes da equação é 4. Com isso basta substituir o valor de q em alguma das equações do sistema e você chegará por puro algebrismo no valor de a1, que é 1/4.
a1=5/(q+q²)=5(4+4²)=5/20=1/4
Com isso, você descobre os valores de a3 e a4:
a3=a1.q²=1/4.4²=4
a4=a1.q³=1/4 .4³=16
a3+ a4=4 + 16=20
Assim, o valor da soma de a3 e a4 é 20.
Convidado- Convidado
 Re: Progressão Geométrica - IDECAN
Re: Progressão Geométrica - IDECAN
Obrigada, Lucasmed!
Muito bom
Tinha feito o raciocínio certo, mas me perdi nas operações com exponenciais e raízes :~
Muito bom
Tinha feito o raciocínio certo, mas me perdi nas operações com exponenciais e raízes :~
andrea_mt- Iniciante
- Mensagens : 5
Data de inscrição : 26/02/2016
Idade : 34
Localização : Campina Grande, PB
 Tópicos semelhantes
Tópicos semelhantes» PROGRESSÃO ARITMÉTICA - IDECAN
» Progressão Aritmética e Progressão Geométrica
» Progressão Aritmética + Progressão Geométrica
» Progressão geométrica e progressão aritmética
» progressao geometrica
» Progressão Aritmética e Progressão Geométrica
» Progressão Aritmética + Progressão Geométrica
» Progressão geométrica e progressão aritmética
» progressao geometrica
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












