(IFF2015)Amperimetro, potência, resistor

O circuito mostrado a seguir é formado por uma bateria, um voltímetro, um amperímetro e por diferentes resistores, associados em paralelo e em série.


Sabendo que a resistência interna da bateria que alimenta esse circuito é de 2,0 Ω, e que a força eletromotriz vale 36 V e considerando que tanto o voltímetro quanto o amperímetro são ideais, responda:
a) Quais são as leituras no amperímetro e voltímetro?
b) Qual é a potência dissipada pelos resistores de 6,0 Ω?
c) Qual é o resistor que dissipa a maior potência dentre os resistores do circuito? E qual é
o valor dessa potência?

Vamos calcular a resistência equivalente para achar a corrente que sai da bateria.
Em cima tem-se uma resistência equivalente para resistores associados em paralelo, mais dois em paralelo do lado direito e mais dois em série em baixo. Assim, temos: Req=2//6//3 + 6//3 + 3 + 4 = 10Ω
Da lei de Pouillet para achar a corrente em um circuito-simples:

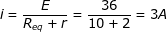
Essa é a corrente que sai da bateria e deve chegar à bateria com mesma intensidade. Então, na associação de três resistores em paralelo lá em cima entra uma corrente de 3A, mas como ela se divide entre eles?

Para achar essa corrente sem usar um sistema de equaçoes, vamos fazer dessa forma: Retira-se o M.M.C. entre os valores das três resistências e o multiplica-se por "x", divide-se então esse número para cada resistor. Esse valor, encontrado para cada resistor, é o da corrente que passa por ele.
Para o nosso caso aqui: 
MMC(2,6,3)=6 --> 6x
Nessa ordem, do resistor de cima para baixo, as correntes são:
Resistor de 2,0Ω : 6x÷2=3x
Resistor de 6,0Ω : 6x÷6=x
Resistor de 3,0Ω : 6x÷3=2x
A soma dessas correntes, 3x+x+2x deve ser igual a 3A, então x=0,5

a)Nesse resistor passa uma corrente de x=0,5A, que é a leitura do amperímetro.
A mesma corrente de 3A sai dessa associação de três resistores e entra pela segunda, para achar a corrente que passa por cada resistor, prosseguimos da mesma forma.
MMC(6,3)=6-->6x
Resistor de 6,0Ω : 6x÷6=x
Resistor de 3,0Ω : 6x÷3=2x
Portanto, x+2x=3A --->x=1A
No resistor de 6Ω passa x=1A, portanto, da lei de Ohm, a ddp entre seus polos (que é a mesma para o outro resistor em parelo com ele!) é dada por:
 U=6Ω*1A=6V

Igualmente sai dessa associação uma corrente de 3A que entra no resistor de 4,0Ω, em seguida. Da lei de Ohm para este resistor, sua ddp é de U'=4,0Ω*3A =12V
A voltagem que o voltímetro mede é dada pela soma dessas voltagens entre os pontos aos quais está ligado, ou seja : U+U'=6V+12V=18V

b) A potência dissipada por um resistor é dada por Pot=r*i².
Para o resistor lá em cima: Pot=6*(0,5)²=1,5W
Para o outro resistor : Pot'=6*(1)²=6W

c) No resistor de 4,0Ω : Pot=4*(3)²=36W


(Talvez tenha ficado um pouco longo neh, desculpe, espero que possa entender  :tongue:)

Um outro modo de calcular as correntes no paralelo 2//6//3

Resistor equivalente deste paralelo ----> R'1 = 1 ohm
Tensão em cada resistor deste paralelo ---> U1 = R'1.i ---> U'1 = 1.3 ---> U'1 = 3 V

Corrente em cada resistor:

i(2) = 3/2 ---> i(2) = 1,5 A
i(6) = 3/6 ---> i(6) = 0,5 A
i(3) = 3/3 ---> i(3) = 1,0 A

Muito boa a explicação obrigada