(UFPE)

Seja x a medida em radianos de ângulo satisfazendo 0 < x < (π/2), como indicado na ilustração abaixo:



Considerando as áreas das diferentes regiões da figura, analise as afirmações seguintes:

(01) sen x < x < tg x
(02) 1 - cos x = sen² x / (1 + cos x) < x²
(03) cos x < sen x / x < 1
(04) 1 - x² < sen x / x < 1

Gabarito: V/V/V/V

Alguém poderia me ajudar nessa questão?

Desde já, eu agradeço.

Sejam:

O = origem
C = encontro do arco com o eixo x
D = encontro do arco com o eixo y
H = pé da perpendicular de B sobre o eixo x

OH = cosx ---> BH = senx ---> AC = tgx ---> x = arco BC ---> 1 - cosx = CH

sen²x = 1 - cos²x

1 + cosx = 2.cos²(x/2)

Basta comparar comprimentos

Essa questão é linda porque, se você entrar num curso de exatas, essa figura é capital para você poder definir um dos limites mais fundamentais do cálculo. Vamos resolvê-la e depois coloco o limite pra você também


Seja a origem dos centros o ponto O. Traçamos uma reta BC, tal que: 




Vamos calcular as seguintes áreas:

OBC, OAC e o setor circular formado pelo angulo X.

É de imediato que as áreas tem a relação:



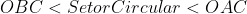
Calculemos a área de OBC:

Temos que h de OBC é dada por:



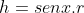
Como r = 1, então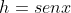 

Logo, a área de OBC é: 



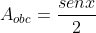
Calculemos a área do Setor Circular:

Temos que a área de um setor circular é dado por:



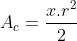
Então, .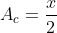

Calculemos OAC:


Observamos que AC = tanx.

Assim,

.


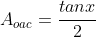Da relação de desigualdade entre as áreas, temos então:




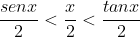
Multiplicamos tudo por 2, logo temos que (01) é verdadeira:

.

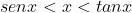Avaliemos a afirmação (02) ao manipulá-la:



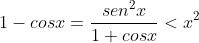
Então, 



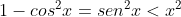
Ora, com efeito, se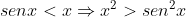 . Logo, (02) é verdadeira também.

Da relação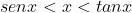 ., vamos dividi-la por senx. Então,



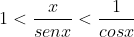
Invertendo as frações, temos:

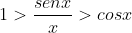 . Logo (03) é verdadeira.

Pela figura, seja O' a distância da origem até a altura do triângulo OBC.

Temos que 

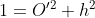 . Como h = senx, então:



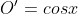
Para que a última afirmação verdadeira, dada a veracidade da relação anterior, a saber,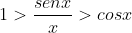   nos é obrigado a admitir que 

.

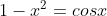No entanto, pela figura temos que cosx<1

Então,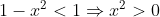  o que é verdade, uma vez que x equivale ao arco BC e este é maior que 0. Logo tal afirmação é verdadeira.

Assim, as verdadeiras são 01,02,03,04.


Agora vamos ao limite fundamental do cálculo

Há um teorema em cálculo que afirma que:

Sejam f,g,h funções contínuas tais que .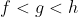


(na figura a relação é h
Se tomarmos os limites dos extremos, isto é, limite tanto de f quanto de h, e se esses limites são coincidentes, então o limite de g é obrigado também a ter esse mesmo valor.


Assim, da nossa relação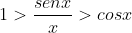  , tomemos o limite de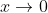 

Então,



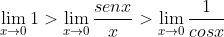
Temos que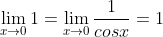 


Logo, pelo teorema do confronto, .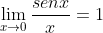

Esse limite é bastante utilizado em cálculo!

Obrigado, Elcioschin e maico33LP!