Divisão em partes iguais

por Matheus José Qua 30 Dez 2015, 11:40

Determine os pontos que dividem AB em quatro partes iguais quando A(-1,-3) e B(23,33).

por **Carlos Adir** Qua 30 Dez 2015, 13:30

Uma maneira de resolução é a utilização de vetores. Isto é, temos o vetor AB:
$\vec{\mathrm{AB}}=\mathrm{\left(x_b-x_a, \ y_b-y_a \right )}$
E o vetor AP:
$\vec{\mathrm{AP}}=\mathrm{\left(x-x_a, \ y-y_a \right )}$
Como os vetores são paralelos, então temos que um será multiplo do outro. E se estamos considerando que P está entre A e B, então o vetor AP é menor que AB, o que faz com que AP * r = AB, sendo r > 1. Logo:
$\\ \mathrm{r} \cdot \vec{\mathrm{AP}}=\vec{\mathrm{AB}} \\ \mathrm{r \cdot \left(x-x_a, \ y-y_a \right )=\left(x_b-x_a, \ y_b-y_a \right )} \\ \begin{cases}\mathrm{r \cdot \left(x-x_a \right )=x_b-x_a} \\ \mathrm{r \cdot (y-y_a)=y_b-y_a} \end{cases} \\ \begin{cases}\mathrm{x = \dfrac{x_b-x_a}{r}+x_a} \\ \mathrm{y=\dfrac{y_b-y_a}{r}+y_a} \end{cases}$

Agora, sabemos a coordenada para isso.
Então, vamos aos seguintes casos:
Se r=1, então AP = AB, o que faz com que o ponto P seja coincidente com o ponto B
Se r<1, então AP é maior que AB, o que faz com que o ponto P não esteja entre A e B.
Se r=2, então AP é a metade de AB, e então P é o ponto médio de A e B.
Se r=3, então AP é tres vezes menor que AB, e então o ponto P está a 1/3 de distância de A, e 2/3 de distância de B.
Se r=3/2, então P está a 1/3 de distância de B, e 2/3 de distância de A.

Usando os dados da questão, temos:
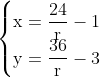
$\begin{cases}\mathrm{x = \dfrac{24}{r}-1} \\ \mathrm{y=\dfrac{36}{r}-3} \end{cases}$
Os pontos que dividem em 4 partes iguais ocorrerá quando r=4, r=4/2, r=4/3. Por consequência, os pontos:
$\mathrm{\left(5, \ 6 \right ); \ \ \left(11, \ 15 \right ); \ \ \left(7, \ 24 \right )}$

por Matheus José Qua 30 Dez 2015, 14:36

Acabei chegando na resposta por dois métodos diferentes, um extremamente: simples, dividir a diferença entre os X dos pontos por 4 e ir somando ao menor X e a mesma coisa com o Y. Mas não entendi sua resolução, começando da representação do vetor,
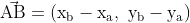
$Divisão em partes iguais Gif$

por **Medeiros** Qui 31 Dez 2015, 05:23

Matheus, seu modo de resolução é correto.

O Carlos Adir aproveitou os conhecimentos de álgebra vetorial para resolver de forma mais simples e rápida -- veja abaixo que fiz a mesma resolução diretamente, sem a explicação literal dada pelo Carlos, e fica bem mais rápido. Sua dificuldade é que não conhece vetores, ainda. Segue uma explicação suscita da teoria e aplicação neste caso.

Um vetor é um ente que tem direção, sentido e módulo. Se temos dois pontos A e B, podemos, a partir das coordenadas destes pontos, definir um vetor AB cuja função é levar do ponto A até o ponto B. Note que nisto já está implícito uma direção (a da reta AB), um sentido (de A para B) e um módulo (a medida do segmento AB). Poderíamos também definir o vetor BA cuja única diferença seria o sentido de B para A.

Como queremos dividir o segmento AB em quatro partes iguais e tendo o vetor AB, dividimos este vetor por 4 e chamamos de vetor r, que terá a mesma direção do vetor AB. Assim, partindo de A (o ponto de partida é importante por causa do sentido do vetor), basta somar r para obtermos o ponto K. E sucessivamente. É claro que somando quatro vezes o vetor r, desta forma, chegaremos ao ponto B originalmente fornecido. Veja a resolução:

Divisão em partes iguais X2pgdg

Poderíamos também, para encontrar os outros pontos, somar a quantidade necessária de vezes o vetor r às coordenadas de A.
L = A + 2.r ........................ e 2.r = 2.(6, 9) = (12, 18)
M = A + 3.r .......................... 3.r = 3.(6, 9) = (18, 27)