Lados de uma Pirâmide

por **Eduardo Sicale** Sex 26 Nov 2010, 20:36

Determine os lados da base de uma pirâmide reta quadrangular, conhecidas a altura h e a superfície lateral 45.

Resposta: x = (-2a²h² + 2*(h elevado a 4 + 45²)^2)^2

Correção da resposta: x = (-2a²h² + 2*(h^4 + 45²)^1/2)^1/2

por **arimateiab** Sex 26 Nov 2010, 22:08

"a superfície lateral 45"
Não entendi :X

por **Elcioschin** Sex 26 Nov 2010, 22:41

x = lado da base (quadrada)
h = altura da pirâmide
A = apótema de cada face lateral da pirâmide

A² = h² + (x/2)² ---> A² = h² + x²/4 ----> 4A² = (4h² + x²)

A área lateral da pirâmide é igual a soma das 4 áreas das superfícies laterais (que são triângulos de base x a altura A):

S = 4*(x*A/2) ----> S = 2*x*A -----> 45 = 2*A*x ----> 45² = 4A²*x² -----> 45² = (4h² + x²)*x² ---->

(x²)² + 4h²(x²) - 45² = 0 ----> Equação do 2º grau na variável x² (ou equção biquadrada)

Discriminante ----> D = (4h²)² - 4*1*-45²) ----> D = 16*h^4 + 4*45² -----> D = 4*(4*h^4 + 45²)

Raiz positiva -----> x2 = [- 4h² + 2*V(4h^4 + 45²)]/2*1 ----> x² = - 2h² + V(4h^4 + 45²)

x = V[ - 2h² + V(4h^4 + 45²)] ----> x = [ - 2h² + (4h^4 + 45²)^(1/2)]^(1/2)

Existem alguns erros no gabarito:

1) Aparece a² junto de 2h² ----> Este a² não existe pois não é um dado do problema

2) Os expoentes estão errados (2). O correto é 1/2 por se tratar de raiz quadrada

3) O número antes de h^4 é 4 (e não 2)

4) O parenteses antes de h^4 deve ficar antes do 4 (ele está errado depois do 2)

por **Eduardo Sicale** Dom 28 Nov 2010, 14:56

Ok, Elcioschin. Desculpe por colocar de forma errada o símbolo da raiz quadrada (o certo é ^1/2 e não ^2). Tive um lapso de memória na hora de digitar a questão. Quanto ao "a", realmente não é dado do problema. Pensei que talvez fosse a aresta lateral da pirâmide, e tentei por várias vezes resolver a questão considerando assim, mas não cheguei no resultado do gabarito. Na verdade, consegui chegar no resultado que você chegou, mas como ainda sou aprendiz da matemática, fiquei na dúvida se não estaria me equivocando em alguma coisa. Agora vi que não me equivoquei, e fiquei feliz por isso. Essa questão foi realmente muito mal-formulada. Abraços e muito obrigado, mais uma vez !!! Eduardo.

por **adriano tavares** Dom 28 Nov 2010, 15:27

Olá,Eduardo Sicale.

Se eu não estiver enganado, já resolvi essa questão em outro fórum. E não é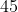 $45$ é $4S$

Um abraço!!!

por **Eduardo Sicale** Dom 28 Nov 2010, 15:37

Olá, Adriano. Você poderia colocar a resolução com 4S ? Talvez seja esse o erro. Abraços !!!

por **adriano tavares** Seg 29 Nov 2010, 19:35

Olá, Eduardo Sicale.

Lados de uma Pirâmide Revisodotpico

A área da superfície lateral é:

$A_{sl}=\frac{4xg}{2}\Rightarrow 4S=\frac{4xg}{2}\Rightarrow x=\frac{2S}{g}$ (I)

Aplicando Pitágoras teremos:

$g^2=h^2+\left(\frac{x}{2} \right )^2 \Rightarrow g^2=\frac{4h^2+x^2}{4}\Rightarrow g=\sqrt{\frac{4h^2+x^2}{4}}g=\frac{\sqrt{4h^2+x^2}}{2}$ (II)

Substituindo (II) em (I)

$x=\frac{2S}{g}\Rightarrow x=\frac{2S}{\frac{\sqrt{4h^2+x^2}}{2}}\Rightarrow x=\frac{4S}{\sqrt{4h^2+x^2}}$

Elevando ambos os membros ao quadrado teremos:

$x^2=\frac{16S^2}{4h^2+x^2} \Rightarrow x^4+4h^2x^2=16S^2\\\\ (x^2)^2+4h^2x^2-16S^2=0$

Fazendo-se x²=y teremos:

$y^2+4h^2y-16S^2=0$

Resolvendo essa equação do 2ºgrau encontraremos:

$y_1=-2h^2+2\sqrt{h^4+4S^2}\\\\y_2=-2h^2-2\sqrt{h^4+4S^2}$

Vamos desconsiderar o valor de y_2, pois ele é menor que zero.

Substituindo teremos:

$x^2=y \Rightarrow x=\sqrt{y_1}\Rightarrow x=\sqrt{-2h^2+2\sqrt{h^4+4S^2}}$