Construção de gráfico

O gráfico abaixo representa uma função do 1º grau do tipo f(x) = ax + b, definida de
ℜ em ℜ, observe:

Como é o gráfico que representa h(x) = |f(x)| + 2

Neste tipo de exercício, analise a nova função pedida por partes.

1) f(4)=0  >>> a.4+b=0
    f(0)=6 >>>b=6
 Do sistema tem-se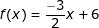

2) Para |f(x)|, note que conforme o módulo sempre deixa a imagem positiva, o eixo dos Y não deve ter valores negativos e a reta da função nunca passa "embaixo", simplesmente "rebatemos" essa reta de negativos para cima.


3) Ao adicionar 2, devemos mover o gráfico duas unidades pra cima no eixo Y, de modo que a imagem sempre esteja somada a 2.

Esse é o gráfico pedido, veja que corta o eixo Y quando f(0)=8 e o vértice da função continua sobre uma mesma vertical, passando a ser o ponto (4;2)